Pythagorean theorem - math word problems - page 34 of 73
Number of problems found: 1451
- Embankment 7879
 An embankment 7.5 m high should be built on the horizontal plane. The width of the upper surface of the embankment is 2.9 m, and the slope is 35 °. What will be the lower width of the embankment?
An embankment 7.5 m high should be built on the horizontal plane. The width of the upper surface of the embankment is 2.9 m, and the slope is 35 °. What will be the lower width of the embankment? - Simultaneously 82583
 The crane lifts the load in a uniform, straight line to a height of 8 m and simultaneously moves in a horizontal direction to a distance of 6 m. What path did the load cover? What was the resulting velocity of the load if it took 50 seconds to move it
The crane lifts the load in a uniform, straight line to a height of 8 m and simultaneously moves in a horizontal direction to a distance of 6 m. What path did the load cover? What was the resulting velocity of the load if it took 50 seconds to move it - Circumference 66134
 The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid.
The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid. - Position 19113
 The column is fixed in a vertical position by 3 ropes, which are caught at the height of 3 m above the ground. The other ends of the ropes are anchored to the ground at a distance of 4 m from the base of the column. How much rope was used to secure the po
The column is fixed in a vertical position by 3 ropes, which are caught at the height of 3 m above the ground. The other ends of the ropes are anchored to the ground at a distance of 4 m from the base of the column. How much rope was used to secure the po - Cross-section 4343
 Premium quality olive oil is sold in a glass bottle with a square cross-section packed in a special cylinder tube. The square's perimeter that forms the bottle's cross-section is 28 cm. What is the radius of this tube?
Premium quality olive oil is sold in a glass bottle with a square cross-section packed in a special cylinder tube. The square's perimeter that forms the bottle's cross-section is 28 cm. What is the radius of this tube? - RRL Basics
 What is the length of the smaller base of an isosceles trapezoid and the height, if a = 9 dm, the side is 6 dm and the angle ACB is 90 degrees?
What is the length of the smaller base of an isosceles trapezoid and the height, if a = 9 dm, the side is 6 dm and the angle ACB is 90 degrees? - PT - Pythagorean
 A right triangle ABC has hypotenuse c and legs a, and b of the following lengths. Estimate the length of its remaining side and compare your estimates with your calculations. a) a = 4 cm; b = 5 cm b) a = 6.8 m; b = 9 m c) a= 8.9 m; b = 1 m d) b= 10 cm; c
A right triangle ABC has hypotenuse c and legs a, and b of the following lengths. Estimate the length of its remaining side and compare your estimates with your calculations. a) a = 4 cm; b = 5 cm b) a = 6.8 m; b = 9 m c) a= 8.9 m; b = 1 m d) b= 10 cm; c - Right triangle generator
 Detective Harry Thomson found on the Internet a generator of the lengths of the sides of right triangles according to which he must apply: a = 2xy, b = x² - y², c = x² + y², where are natural numbers and x & gt; y. Is it a working generator?
Detective Harry Thomson found on the Internet a generator of the lengths of the sides of right triangles according to which he must apply: a = 2xy, b = x² - y², c = x² + y², where are natural numbers and x & gt; y. Is it a working generator? - Altitude angles
 Cities A, B, and C lie in one elevation plane. C is 50 km east of B, and B is north of A. C is deviated by 50° from A. The plane flies around places A, B, and C at the same altitude. When the aircraft is flying around B, its altitude angle to A is 12°. Fi
Cities A, B, and C lie in one elevation plane. C is 50 km east of B, and B is north of A. C is deviated by 50° from A. The plane flies around places A, B, and C at the same altitude. When the aircraft is flying around B, its altitude angle to A is 12°. Fi - Garden G
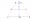 The rectangular, trapezoidal garden has a base length of 81m, 76m, and a vertical arm of 12m. Calculate how many m² of the area will remain for planting greenery if 1/3 of the area is built. Calculate the consumption of mesh for land fencing.
The rectangular, trapezoidal garden has a base length of 81m, 76m, and a vertical arm of 12m. Calculate how many m² of the area will remain for planting greenery if 1/3 of the area is built. Calculate the consumption of mesh for land fencing. - Free space in the garden
 The grandfather's free space in the garden was in the shape of a rectangular triangle of 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. The smaller part creates a rock garden, for the larger sows
The grandfather's free space in the garden was in the shape of a rectangular triangle of 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. The smaller part creates a rock garden, for the larger sows - Triangular pyramid
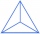 A regular tetrahedron is a triangular pyramid whose base and walls are identical equilateral triangles. Calculate the height of this body if the edge length is a = 8 cm.
A regular tetrahedron is a triangular pyramid whose base and walls are identical equilateral triangles. Calculate the height of this body if the edge length is a = 8 cm. - Laths
 There are two laths in the garage opposite one another: one 2 meters long and the other 3 meters long. They fall against each other and lean against the opposite walls of the garage. Both laths touch at 70 cm above the garage floor. How wide is the garage
There are two laths in the garage opposite one another: one 2 meters long and the other 3 meters long. They fall against each other and lean against the opposite walls of the garage. Both laths touch at 70 cm above the garage floor. How wide is the garage - Parallelogram - area
 Calculate the area of the parallelogram if the sides are a = 80, b = 60 long, and the size of the diagonal angle is 60°.
Calculate the area of the parallelogram if the sides are a = 80, b = 60 long, and the size of the diagonal angle is 60°. - 30-gon
 The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area.
The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area. - 6 regular polygon
 A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon.
A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon. - Rectangle and circle
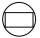 The rectangle ABCD has side lengths a = 40 mm and b = 30 mm and is circumscribed by a circle k. Calculate approximately how many centimeters a circle is long.
The rectangle ABCD has side lengths a = 40 mm and b = 30 mm and is circumscribed by a circle k. Calculate approximately how many centimeters a circle is long. - Trapezoid RT
 The plot is a rectangular trapezium ABCD, where ABIICD has a right angle at the vertex B side and AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. The lengths of the sides AB and CD are in the ratio 3:2. Calculate the con
The plot is a rectangular trapezium ABCD, where ABIICD has a right angle at the vertex B side and AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. The lengths of the sides AB and CD are in the ratio 3:2. Calculate the con - Garden
 The square garden area is 2/9 of a triangle garden with sides 160 m, 100 m, and 100 m. How many meters of fencing are needed to fence a square garden?
The square garden area is 2/9 of a triangle garden with sides 160 m, 100 m, and 100 m. How many meters of fencing are needed to fence a square garden? - Glass mosaic
 How many dm² glasses are necessary to produce 97 slides of a regular 6-gon, whose side has a length of 21 cm? Assume that cutting glass waste is 10%.
How many dm² glasses are necessary to produce 97 slides of a regular 6-gon, whose side has a length of 21 cm? Assume that cutting glass waste is 10%.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
