Pythagorean theorem - practice problems - page 9 of 73
Number of problems found: 1451
- Diagonals
 The rhombus has two diagonals, e=14 dm, and f=11 dm. Calculate the side angle and height of the rhombus.
The rhombus has two diagonals, e=14 dm, and f=11 dm. Calculate the side angle and height of the rhombus. - Arm
 Calculate the length of the arm r of isosceles triangle ABC, with base |AB| = 14 cm and a height v=18 cm.
Calculate the length of the arm r of isosceles triangle ABC, with base |AB| = 14 cm and a height v=18 cm. - Diagonal
 Calculate the diagonal length of the rectangle ABCD with sides a = 7 cm, b = 10 cm.
Calculate the diagonal length of the rectangle ABCD with sides a = 7 cm, b = 10 cm. - Q-Exam
 If tg α = 8.6, Calculating sin α, cos α, cotg α .
If tg α = 8.6, Calculating sin α, cos α, cotg α . - Proof PT
 Can you easily prove Pythagoras' theorem using Euclidean theorems? If so, do it.
Can you easily prove Pythagoras' theorem using Euclidean theorems? If so, do it. - Diagonals of the rhombus
 Calculate the height of the rhombus whose diagonals are 18 cm and 6 cm.
Calculate the height of the rhombus whose diagonals are 18 cm and 6 cm. - Calculate 82490
 Calculate the area of an isosceles triangle ABC with a base of 10 cm and a side of 7 cm. Sketch a picture.
Calculate the area of an isosceles triangle ABC with a base of 10 cm and a side of 7 cm. Sketch a picture. - Isosceles 9881
 The area of an isosceles right triangle is 32 cm square. What is his circuit?
The area of an isosceles right triangle is 32 cm square. What is his circuit? - Distance 7717
 To what height does a 6.5 m long ladder leaning against a wall at a distance of 5.4 m reach?
To what height does a 6.5 m long ladder leaning against a wall at a distance of 5.4 m reach? - Circumscribed 7290
 Calculate the area of a regular hexagon if the radius of the circle circumscribed is 6.8 cm.
Calculate the area of a regular hexagon if the radius of the circle circumscribed is 6.8 cm. - Equilateral 5571
 The height in the equilateral triangle ABC measures the square root of 3 cm. What is the length of the center bar of this triangle?
The height in the equilateral triangle ABC measures the square root of 3 cm. What is the length of the center bar of this triangle? - Calculate 5255
 The area of the square is equal to 2.56 square meters. Calculate its diagonal.
The area of the square is equal to 2.56 square meters. Calculate its diagonal. - Embankment 2539
 The profile of the railway embankment has the shape of an isosceles trapezoid, where a = 16.4 m, c = 10.6 m, and b = d = 5.2 m. Calculate the embankment height.
The profile of the railway embankment has the shape of an isosceles trapezoid, where a = 16.4 m, c = 10.6 m, and b = d = 5.2 m. Calculate the embankment height. - Arbor
 Calculate in square meters the area of an arbor whose ground plan is in the shape of a regular hexagon with a side length of 4.5 m.
Calculate in square meters the area of an arbor whose ground plan is in the shape of a regular hexagon with a side length of 4.5 m. - Chord and radius
 Calculate the radius of a circle whose chord XY is 8 cm long and whose center is 3 cm from the chord.
Calculate the radius of a circle whose chord XY is 8 cm long and whose center is 3 cm from the chord. - Height - the ladder
 At what height does the 15 m ladder touch the wall if its lower end is 2.5 m away from it?
At what height does the 15 m ladder touch the wall if its lower end is 2.5 m away from it? - RT triangle and height
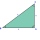 Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm.
Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm. - Spruce height
 How tall was the spruce that was cut at an altitude of 8m above the ground, and the top landed at a distance of 15m from the heel of the tree?
How tall was the spruce that was cut at an altitude of 8m above the ground, and the top landed at a distance of 15m from the heel of the tree? - Is right triangle or not
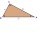 If the right triangle is ABC, it has sides a=13, b=11.5, and c=22.5. Find area.
If the right triangle is ABC, it has sides a=13, b=11.5, and c=22.5. Find area. - Diagonals in diamons/rhombus
 Rhombus ABCD has a side length AB = 4 cm and a length of one diagonal of 6.4 cm. Calculate the length of the other diagonal.
Rhombus ABCD has a side length AB = 4 cm and a length of one diagonal of 6.4 cm. Calculate the length of the other diagonal.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
