Right triangle practice problems - page 74 of 86
Number of problems found: 1720
- Sphere submerged in the cone
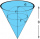A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere. - A transmitter tower
A transmitter tower is 80 meters high and is stabilized to the ground by 4 steel cables anchored in the ground 60 meters from the base of the tower. Calculate how many meters of steel cable were needed to stabilize the transmitter tower. The steel cable u - A plane vs. sphere
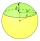The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere. - Tetrahedral pyramid
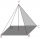A regular tetrahedral pyramid is given. Base edge length a = 6.5 cm, side edge s = 7.5 cm. Calculate the volume and the area of its face (side area). - Calculate 6566
Calculate the surface area and volume of a regular hexagonal pyramid whose base edge is 10 cm long and the side edge is 26 cm long. - Calculate 6331 The regular hexagonal pyramid has a base edge of 20 cm and a side edge of 40 cm. Calculate the height and surface of the pyramid
- Segment
Calculate the segment AB's length if the coordinates of the end vertices are A[0, -2] and B[-4, 9]. - Square inscribed
Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm. - Hexagonal pyramid
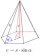A regular hexagonal pyramid has dimensions: the length edge of the base a = 1.8 dm, and the height of the pyramid = 2.4 dm. Calculate the surface area and volume of a pyramid. - Dodecagon
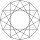Find the area of a regular dodecagon (n=12) if the radius of the circumscribed circle is 5 cm. - Horizon
The top of a lighthouse is 18 m above the sea. How far away is an object just "on the horizon"? [Assume the Earth is a sphere of radius 6378.1 km.] - Magnitude 25411
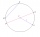There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord. - Tetrahedral pyramid
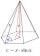It is given a regular tetrahedral pyramid with a base edge of 6 cm and a height of pyramid 10 cm. Calculate the length of its side edges. - Base RR odd
The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm. - ABCDEFGH 82499
In the cube ABCDEFGH, the area of triangle ABK is √20 cm². How much cm² is the volume of ABGH in a cube if you know that K is the midpoint of edge CG? - Triangle IRT
An isosceles right triangle ABC with a right angle at vertex C has vertex coordinates: A (-1, 2); C (-5, -2). Calculate the length of segment AB. - Quadrilateral 8109
The regular quadrilateral pyramid has a base diagonal of 5√2 cm, and the side edges are 12√2 cm long. Calculate the height of the pyramid and its surface. - Quadrilateral pyramid
We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm. Calculate 1/base area 2/casing area 3/pyramid surface 4/volume of the pyramid - Triangular prism
The base perpendicular triangular prism is a right triangle whose hypotenuse measures 14 cm and one cathetus 9 cm. The height of the prism is equal to 2/9 of the base's perimeter. Calculate the surface area of the prism. - Regular quadrilateral pyramid
Find the surface area of a regular quadrilateral pyramid if for its volume V and body height v and the base edge, a applies: V = 2.8 m³, v = 2.1 m
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
