Square (second power, quadratic) - math word problems - page 132 of 150
Number of problems found: 2994
- Velocity ratio
 Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the flui
Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the flui - Rhombus 2
 Calculate the rhombus area with a height v=48 mm and shorter diagonal u = 60 mm long.
Calculate the rhombus area with a height v=48 mm and shorter diagonal u = 60 mm long. - Cardboard box
 We want to make a cardboard box-shaped quadrangular prism with a rhombic base. The rhombus has a side of 5 cm and 8 cm, one diagonal long. The height of the box is 12 cm. The box will be open at the top. How many square centimeters do we need if we calcul
We want to make a cardboard box-shaped quadrangular prism with a rhombic base. The rhombus has a side of 5 cm and 8 cm, one diagonal long. The height of the box is 12 cm. The box will be open at the top. How many square centimeters do we need if we calcul - Square plate
 The locksmith cut a square metal plate with a sidelong 6 dm into two identical rectangular openings with 2.5 dm and 2 dm dimensions. Calculate the remainder of the square plate.
The locksmith cut a square metal plate with a sidelong 6 dm into two identical rectangular openings with 2.5 dm and 2 dm dimensions. Calculate the remainder of the square plate. - Rhomboid
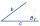 The rhomboid sides' dimensions are a= |AB|=5cm, b = |BC|=6 cm, and the angle's size at vertex A is 60°. What is the length of the diagonal AC?
The rhomboid sides' dimensions are a= |AB|=5cm, b = |BC|=6 cm, and the angle's size at vertex A is 60°. What is the length of the diagonal AC? - Rope slack
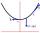 Between two streets, 20 m away, give the lamp in the middle and hang 60 cm below the taut rope. Can it be done with a 20.5 meters rope?
Between two streets, 20 m away, give the lamp in the middle and hang 60 cm below the taut rope. Can it be done with a 20.5 meters rope? - Circumference 1608
 The bases of the isosceles trapezoid measure 110m and 50m. The distance between the bases is 40m. Calculate its circumference.
The bases of the isosceles trapezoid measure 110m and 50m. The distance between the bases is 40m. Calculate its circumference. - Rotary cylinder
 The rotating cylinder has a surface area of 69.08 cm². The area of the shell is 62.8 cm ². What is the diameter of the cylinder?
The rotating cylinder has a surface area of 69.08 cm². The area of the shell is 62.8 cm ². What is the diameter of the cylinder? - Greenhouse
 The Garden plastic greenhouse is shaped like a half-cylinder with a diameter of 6 m and a base length of 20 m. At least how many m² of plastic is needed for its cover?
The Garden plastic greenhouse is shaped like a half-cylinder with a diameter of 6 m and a base length of 20 m. At least how many m² of plastic is needed for its cover? - Water
 The lawn has an area 1571 m², rained 5 mm of water. How many liters of water rained?
The lawn has an area 1571 m², rained 5 mm of water. How many liters of water rained? - Tent
 A pyramid-shaped tent has a base square with a side length of 2 m and a height of 1.7 m. How many meters of canvas is needed to make it if we should add 10% for waste?
A pyramid-shaped tent has a base square with a side length of 2 m and a height of 1.7 m. How many meters of canvas is needed to make it if we should add 10% for waste? - Bottles of juice
 How many 2-liter bottles of juice need to buy if you want to transfer the juice to 50 pitchers' rotary cone shape with a diameter of 24 cm and a base side length of 1.5 dm?
How many 2-liter bottles of juice need to buy if you want to transfer the juice to 50 pitchers' rotary cone shape with a diameter of 24 cm and a base side length of 1.5 dm? - 3d vector component
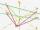 The vector u = (3.9, u3), and the length of the vector u is 12. What is, is u3?
The vector u = (3.9, u3), and the length of the vector u is 12. What is, is u3? - Trapezoid - hard example
 Bases of the trapezoid are: 24, 16 cm. Diagonal 22, 26 cm. Calculate its area and perimeter.
Bases of the trapezoid are: 24, 16 cm. Diagonal 22, 26 cm. Calculate its area and perimeter. - Triangle midpoints
 Determine coordinates of triangle ABC vertices if we know triangle sides midpoints SAB [0;3] SBC [1;6] SAC [4;5], its sides AB, BC, AC.
Determine coordinates of triangle ABC vertices if we know triangle sides midpoints SAB [0;3] SBC [1;6] SAC [4;5], its sides AB, BC, AC. - Percentage of waste
 In a square plate with a side 58 cm, we cut four same circles. Calculate the percentage of waste.
In a square plate with a side 58 cm, we cut four same circles. Calculate the percentage of waste. - Square and circle
 Into the square is an inscribed circle with a diameter of 10 cm. What is the difference between a circumference square and a circle?
Into the square is an inscribed circle with a diameter of 10 cm. What is the difference between a circumference square and a circle? - Concentric circles
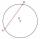 In the circle with diameter, 13 cm is constructed chord 1 cm long. Calculate the radius of a concentric circle that touches this chord.
In the circle with diameter, 13 cm is constructed chord 1 cm long. Calculate the radius of a concentric circle that touches this chord. - Again saw
 We have a sculpture beam from the tree trunk with a rectangular cross-section with dimensions 91 mm and 87 mm. What is the trunk's smallest diameter?
We have a sculpture beam from the tree trunk with a rectangular cross-section with dimensions 91 mm and 87 mm. What is the trunk's smallest diameter? - The chord
 Calculate a chord length where the distance from the circle's center (S, 24 cm) equals 16 cm.
Calculate a chord length where the distance from the circle's center (S, 24 cm) equals 16 cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
