Surface Area Calculation Problems for Solid Shapes. - page 30 of 52
Number of problems found: 1029
- Dimensions 3408
 The room has 4m, 5m, and 2.4m dimensions. Suppose one can is enough to paint 10 m². How many cans of paint are needed to paint the walls and ceiling of this room?
The room has 4m, 5m, and 2.4m dimensions. Suppose one can is enough to paint 10 m². How many cans of paint are needed to paint the walls and ceiling of this room? - Axial cut
 The cone surface is 388.84 cm2, and the axial cut is an equilateral triangle. Find the cone volume.
The cone surface is 388.84 cm2, and the axial cut is an equilateral triangle. Find the cone volume. - Hip-roof
 The roof consists of two isosceles trapezoids and two isosceles triangles. The roof plan is a rectangle with dimensions of 8m and 14m, and the roof ridge is 8m long. The height of the trapezoid is 5m, the height of the triangles is 4.2m. How many tiles ar
The roof consists of two isosceles trapezoids and two isosceles triangles. The roof plan is a rectangle with dimensions of 8m and 14m, and the roof ridge is 8m long. The height of the trapezoid is 5m, the height of the triangles is 4.2m. How many tiles ar - The rotation cone
 The rotation cone with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume.
The rotation cone with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume. - Dimensions - cardboard
 The statements are sold in cardboard boxes – for example, the microwave oven box has dimensions of 52 cm, 32 cm, and 40 cm, and 0.4 m² of cardboard is added to the folds. How many square meters of cardboard are needed for 1,000 boxes?
The statements are sold in cardboard boxes – for example, the microwave oven box has dimensions of 52 cm, 32 cm, and 40 cm, and 0.4 m² of cardboard is added to the folds. How many square meters of cardboard are needed for 1,000 boxes? - Triangular prism
 The regular triangular prism has a base edge of 8.6 dm and a height of 1.5 m. Find its volume and surface area.
The regular triangular prism has a base edge of 8.6 dm and a height of 1.5 m. Find its volume and surface area. - Rotating cone
 If the side of the rotating cone is 150 mm long and the circumference of the base is 43.96 cm, find its surface and volume.
If the side of the rotating cone is 150 mm long and the circumference of the base is 43.96 cm, find its surface and volume. - Sphere parts, segment
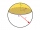 A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment?
A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment? - Regular quadrilateral pyramid
 What is the volume of a regular quadrilateral pyramid if its surface is 576 cm² and the base edge is 16 cm?
What is the volume of a regular quadrilateral pyramid if its surface is 576 cm² and the base edge is 16 cm? - Volleyball - air in ball
 The radius of a volleyball is 10 cm. Calculate how many liters of air fit into an ideal inflated ball. Calculate how many square meters of leather material you need to make it.
The radius of a volleyball is 10 cm. Calculate how many liters of air fit into an ideal inflated ball. Calculate how many square meters of leather material you need to make it. - Two hemispheres
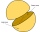 In a wooden hemisphere with a radius r = 1, the carpenter created a hemispherical depression with a radius r/2. The bases of both hemispheres lie in the same plane. What is the surface of the created body (including the surface of the depression)?
In a wooden hemisphere with a radius r = 1, the carpenter created a hemispherical depression with a radius r/2. The bases of both hemispheres lie in the same plane. What is the surface of the created body (including the surface of the depression)? - Cutting the prism
 A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism?
A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism? - Cone roof
 How many m² of roofing is needed to cover a cone-shaped roof with a diameter of 10 m and a height of 4 m? Add an extra 4% to the overlays.
How many m² of roofing is needed to cover a cone-shaped roof with a diameter of 10 m and a height of 4 m? Add an extra 4% to the overlays. - Quadrilateral pyramid
 In a regular quadrilateral pyramid, the side edge is e = 7 dm, and the base's diagonal is 50 cm. Calculate the pyramid shell area.
In a regular quadrilateral pyramid, the side edge is e = 7 dm, and the base's diagonal is 50 cm. Calculate the pyramid shell area. - Seat
 How much m² of fabric do we need to sew a 50cm-shaped cube-shaped seat if we add 10% of the material to the folds?
How much m² of fabric do we need to sew a 50cm-shaped cube-shaped seat if we add 10% of the material to the folds? - Pyramid in cube
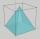 In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid.
In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid. - The roof of the church
 The cone roof of the church has a diameter of 3 m and a height of 4 m. What is the size of the side edge of the church roof (s=?), and how many sheets of the sheet will be needed to cover the church roof?
The cone roof of the church has a diameter of 3 m and a height of 4 m. What is the size of the side edge of the church roof (s=?), and how many sheets of the sheet will be needed to cover the church roof? - Triangular prism
 The base of the perpendicular triangular prism is a right triangle with a leg length of 5 cm. The area of the largest sidewall of its surface is 130 cm², and the body's height is 10 cm. Calculate its volume.
The base of the perpendicular triangular prism is a right triangle with a leg length of 5 cm. The area of the largest sidewall of its surface is 130 cm², and the body's height is 10 cm. Calculate its volume. - Sphere - parts
 Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 8 cm and a height v = 4.2 cm.
Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 8 cm and a height v = 4.2 cm. - Present
 The gift box has a rectangular shape with dimensions of 8×8×3 cm. Miloslav wants to cover it with square paper with sides of 18 cm. How much paper was left to him?
The gift box has a rectangular shape with dimensions of 8×8×3 cm. Miloslav wants to cover it with square paper with sides of 18 cm. How much paper was left to him?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
