Triangle practice problems - page 108 of 126
Number of problems found: 2502
- Trapezoid thirds
 The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment.
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Tetrahedron surface area
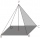
 Calculate the surface of a regular tetrahedron if the length of the wall height v = 1 dm.
Calculate the surface of a regular tetrahedron if the length of the wall height v = 1 dm. - Tetrahedral pyramid
 A regular tetrahedral pyramid is given. Base edge length a = 6.5 cm, side edge s = 7.5 cm. Calculate the volume and the area of its face (side area).
A regular tetrahedral pyramid is given. Base edge length a = 6.5 cm, side edge s = 7.5 cm. Calculate the volume and the area of its face (side area). - Center of line segment
 Calculate the distance of point X [1,3] from the center of the line segment x = 2-6t, y = 1-4t; t is from interval <0,1>.
Calculate the distance of point X [1,3] from the center of the line segment x = 2-6t, y = 1-4t; t is from interval <0,1>. - Triangle IRT
 An isosceles right triangle ABC with a right angle at vertex C has vertex coordinates: A (-1, 2); C (-5, -2). Calculate the length of segment AB.
An isosceles right triangle ABC with a right angle at vertex C has vertex coordinates: A (-1, 2); C (-5, -2). Calculate the length of segment AB. - Square inscribed
 Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm.
Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm. - Octahedron
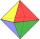 All walls of the regular octahedron are identical equilateral triangles. ABCDEF octahedron edges have a length d = 6 cm. Calculate the surface area and volume of this octahedron.
All walls of the regular octahedron are identical equilateral triangles. ABCDEF octahedron edges have a length d = 6 cm. Calculate the surface area and volume of this octahedron. - Sphere submerged in the cone
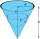 A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere.
A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere. - Hexagon
 Draw a regular hexagon inscribed in a circle with a radius r=15 cm. What is its perimeter?
Draw a regular hexagon inscribed in a circle with a radius r=15 cm. What is its perimeter? - Triangular prism
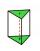 The base perpendicular triangular prism is a right triangle whose hypotenuse measures 14 cm and one cathetus 9 cm. The height of the prism is equal to 2/9 of the base's perimeter. Calculate the surface area of the prism.
The base perpendicular triangular prism is a right triangle whose hypotenuse measures 14 cm and one cathetus 9 cm. The height of the prism is equal to 2/9 of the base's perimeter. Calculate the surface area of the prism. - A transmitter tower
 A transmitter tower is 80 meters high and is stabilized to the ground by 4 steel cables anchored in the ground 60 meters from the base of the tower. Calculate how many meters of steel cable were needed to stabilize the transmitter tower. The steel cable u
A transmitter tower is 80 meters high and is stabilized to the ground by 4 steel cables anchored in the ground 60 meters from the base of the tower. Calculate how many meters of steel cable were needed to stabilize the transmitter tower. The steel cable u - Tetrahedral pyramid
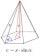 It is given a regular tetrahedral pyramid with a base edge of 6 cm and a height of pyramid 10 cm. Calculate the length of its side edges.
It is given a regular tetrahedral pyramid with a base edge of 6 cm and a height of pyramid 10 cm. Calculate the length of its side edges. - Hexagon
 Calculate the surface area of the regular hexagonal prism, whose base edge a = 12cm and side edge b = 3 dm.
Calculate the surface area of the regular hexagonal prism, whose base edge a = 12cm and side edge b = 3 dm. - Diagonals at right angle
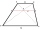 In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD?
In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - Regular quadrilateral pyramid
 Find the surface area of a regular quadrilateral pyramid if for its volume V and body height v and the base edge, a applies: V = 2.8 m³, v = 2.1 m
Find the surface area of a regular quadrilateral pyramid if for its volume V and body height v and the base edge, a applies: V = 2.8 m³, v = 2.1 m - Quadrilateral pyramid
 We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm. Calculate 1/base area 2/casing area 3/pyramid surface 4/volume of the pyramid
We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm. Calculate 1/base area 2/casing area 3/pyramid surface 4/volume of the pyramid - Hexagonal prism
 Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm.
Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm. - Hexagonal pyramid
 Find the volume of a regular hexagonal pyramid, the base edge 12 cm long and the side edge 20 cm.
Find the volume of a regular hexagonal pyramid, the base edge 12 cm long and the side edge 20 cm. - Regular hexagonal pyramid
 Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height of w = 20cm. Sketch a picture.
Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height of w = 20cm. Sketch a picture. - Coordinates of a centroind
 Let A = [3, 2, 0], B = [1, -2, 4], and C = [1, 1, 1] be 3 points in space. Calculate the coordinates of the centroid of △ABC (the intersection of the medians).
Let A = [3, 2, 0], B = [1, -2, 4], and C = [1, 1, 1] be 3 points in space. Calculate the coordinates of the centroid of △ABC (the intersection of the medians).
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
