Triangle practice problems - page 107 of 126
Number of problems found: 2501
- The mast
 A 40 m high mast is secured in half by eight ropes 25 m long. The ends of the ropes are equidistant from each other. Calculate this distance.
A 40 m high mast is secured in half by eight ropes 25 m long. The ends of the ropes are equidistant from each other. Calculate this distance. - The diagram 2
 The diagram shows a cone with a slant height of 10.5cm. If the curved surface area of the cone is 115.5 cm². Calculate to correct three significant figures: *Base Radius *Height *Volume of the cone
The diagram shows a cone with a slant height of 10.5cm. If the curved surface area of the cone is 115.5 cm². Calculate to correct three significant figures: *Base Radius *Height *Volume of the cone - Wall and body diagonals
 Calculate the lengths of the wall and body diagonals of the cuboid with edge dimensions of 0.5 m, 1 m, and 2 m
Calculate the lengths of the wall and body diagonals of the cuboid with edge dimensions of 0.5 m, 1 m, and 2 m - Hexagonal prism 2
 The regular hexagonal prism has a surface of 140 cm² and a height of 5 cm. Calculate its volume.
The regular hexagonal prism has a surface of 140 cm² and a height of 5 cm. Calculate its volume. - Rhombus 47
 A rhombus has a side length of 5 m and a longer diagonal length of 8 m. What is the length of the shorter diagonal of the rhombus?
A rhombus has a side length of 5 m and a longer diagonal length of 8 m. What is the length of the shorter diagonal of the rhombus? - Rectangle
 In a rectangle with sides, 8 and 9 mark the diagonal. What is the probability that a randomly selected point within the rectangle is closer to the diagonal than any side of the rectangle?
In a rectangle with sides, 8 and 9 mark the diagonal. What is the probability that a randomly selected point within the rectangle is closer to the diagonal than any side of the rectangle? - Divide an isosceles triangle
 How can an isosceles triangle be divided into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)?
How can an isosceles triangle be divided into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)? - Right circular cone
 The volume of a right circular cone is 5 liters. The cone is divided by a plane parallel to the base, one-third down from the vertex to the base. Calculate the volume of these two parts of the cone.
The volume of a right circular cone is 5 liters. The cone is divided by a plane parallel to the base, one-third down from the vertex to the base. Calculate the volume of these two parts of the cone. - 10-centimeter-high 7638
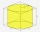 A block with a square base is inserted into a 10-centimeter-high cylinder in such a way that its base is inscribed in the base of the cylinder. The edge of the base of the block measures 4 cm. Both bodies have the same height. Calculate the difference bet
A block with a square base is inserted into a 10-centimeter-high cylinder in such a way that its base is inscribed in the base of the cylinder. The edge of the base of the block measures 4 cm. Both bodies have the same height. Calculate the difference bet - Right-angled trapezoid
 A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is:
A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is: - Quadrilateral 13881
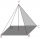 Please calculate the volume of a quadrilateral pyramid when a = 5cm and the wall height is w = 12cm.
Please calculate the volume of a quadrilateral pyramid when a = 5cm and the wall height is w = 12cm. - Prism - box
 The prism's base is a rectangle with a side of 7.5 cm and 12.5 cm diagonal. The volume of the prism is V = 0.9 dm³. Calculate the surface of the prism.
The prism's base is a rectangle with a side of 7.5 cm and 12.5 cm diagonal. The volume of the prism is V = 0.9 dm³. Calculate the surface of the prism. - Quadrilateral - irregular
 Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees
Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees - Common chord
 The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two - Shooter
 The shooter fired at a target from a distance 49 m. The individual concentric circle of targets has radius increments of 1 cm (25 points) by 1 point. The shot was shifted by 16' (angle degree minutes). How many points should he win his shot?
The shooter fired at a target from a distance 49 m. The individual concentric circle of targets has radius increments of 1 cm (25 points) by 1 point. The shot was shifted by 16' (angle degree minutes). How many points should he win his shot? - Calculate 4865
 Calculate the length of the line segment AB, given A [8; -6] and B [4; 2]
Calculate the length of the line segment AB, given A [8; -6] and B [4; 2] - Ladder
 A 4 m long ladder touches the cube 1mx1m at the wall. How high reach on the wall?
A 4 m long ladder touches the cube 1mx1m at the wall. How high reach on the wall? - A transmitter tower
 A transmitter tower is 80 meters high and is stabilized to the ground by 4 steel cables anchored in the ground 60 meters from the base of the tower. Calculate how many meters of steel cable were needed to stabilize the transmitter tower. The steel cable u
A transmitter tower is 80 meters high and is stabilized to the ground by 4 steel cables anchored in the ground 60 meters from the base of the tower. Calculate how many meters of steel cable were needed to stabilize the transmitter tower. The steel cable u - Right triangle from axes
 A line segment has its ends on the coordinate axes and forms a triangle of area equal to 36 square units. The segment passes through the point ( 5,2). What is the slope of the line segment?
A line segment has its ends on the coordinate axes and forms a triangle of area equal to 36 square units. The segment passes through the point ( 5,2). What is the slope of the line segment? - Prism
 Calculate the volume of the rhombic prism. The prism base is a rhombus whose one diagonal is 47 cm, and the edge of the base is 27 cm. The edge length and height of the base of the prism are 4:3.
Calculate the volume of the rhombic prism. The prism base is a rhombus whose one diagonal is 47 cm, and the edge of the base is 27 cm. The edge length and height of the base of the prism are 4:3.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
