Triangle practice problems - page 43 of 125
Number of problems found: 2496
- Short cut
Imagine that you are going to a friend. That path has a length of 120 meter. Then turn doprava and go other 630 meters, and you are at a friend's. The question is, how much will the journey be shorter if you go directly across the field? - Hypotenuse 79904
I have a right triangle, the length of the hypotenuse is c 20, and I only know the side ratio a:b = 2:1. I can't figure out the actual length of the hangers = I'm already an old man, and my brain doesn't work at 100% like it did years ago at school - I co - The truncated
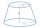The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm, and height v = 5 cm. What is the volume of the cone from which the truncated cone originated? - Candy - MO
Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t - Cross road
From the junction of two streets perpendicular to each other, two cyclists (each on another street) walked out. One ran at 18 km/h, and the second at 24 km/h. How are they away from a) 6 minutes, b) 15 minutes? - Flowerbed
The family has tulips on a square flower bed of 6 meters. Later, they added a square terrace with a side of 7 meters to their house. One vertex of the terrace lay exactly in the middle of a tulip bed, and one side of the terrace was divided by the side of - Movement
Two cyclists (each on a different road) started from the crossing of two perpendicular roads. One runs at an average speed of 16 km/h, and the second 25 km/h. Determine the distance between them after 20 minutes of cycling. - Coefficient 6672
In the triangle ABC is [AB] = 20cm, [BC] = 10cm, A = 30 °. Construct a triangle A'B'C' similar to triangle ABC if the similarity coefficient is 0.5 - Triangle ABC v2
The area of the triangle is 12 cm square. Angle ACB = 30º , AC = (x + 2) cm, BC = x cm. Calculate the value of x. - Lighthouse
The man, 180 cm tall, walks along the seafront directly to the lighthouse. The male shadow caused by the beacon light is initially 5.4 meters long. When the man approaches the lighthouse by 90 meters, its shadow is shorter by 3 meters. How tall is the lig - Calculate 6
Calculate the distance of point A[0, 2] from a line passing through points B[9, 5] and C[1, -1]. - CoG center
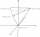Find the position of the center of gravity of a system of four mass points having masses, m1, m2 = 2 m1, m3 = 3 m1, and m4 = 4 m1, if they lie at the vertices of an isosceles tetrahedron. (in all case - Slope of track
Calculate the average slope (in permille and even in degrees) of the rail tracks between Prievidza (309 m AMSL) and Horná štubňa (624 m AMSL) if the track is 37 km long. - Calculating 63344
Calculate the volume of the cone formed by rotating an isosceles triangle about the height of the base. The triangle has a side length of 15 cm and a height to the base of 12 cm. When calculating, use the value pi = 3.14 and round the result to one decima - Square
Calculate the area of the square shape of the isosceles triangle with the arms 50m and the base 60m. How many tiles are used to pave the square if the area of one tile is 25 dm²? - Similarity of squares
The ratio of the similarity of the squares ABCD and KLMN is 2.5. Square KLMN area is greater than an area of a square ABCD with side a: ... - Tin sheet
How much sheet metal is needed for a triangular prism-shaped box with an edge of 20 cm and a height of 30 cm, the height of the base is 15 cm. An additional 10% of sheet metal is needed for gluing. - Determine 82724
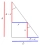A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the area of this square. - In the desert
A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point? - Side deviation
Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
