Triangle - practice for 13 year olds - page 32 of 56
Number of problems found: 1110
- Diamond and diagonals
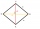 A diamond has diagonals f = 8 cm and g = 6 cm long. How long is this diamond perimeter? (Calculate it!)
A diamond has diagonals f = 8 cm and g = 6 cm long. How long is this diamond perimeter? (Calculate it!) - Rhombus OWES
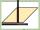 OWES is a rhombus, given that OW is 6cm and one diagonal measures 8cm. Find its area?
OWES is a rhombus, given that OW is 6cm and one diagonal measures 8cm. Find its area? - Rectangle diagonal
 The rectangle, one side of which is 5 cm long, is divided by a 13 cm diagonal into two triangles. Calculate the area of one of these triangles in cm².
The rectangle, one side of which is 5 cm long, is divided by a 13 cm diagonal into two triangles. Calculate the area of one of these triangles in cm². - Draw triangle
 Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37°
Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37°
- Must-have 7893
 If we want to make a prism with a wooden base with a 5 cm side of a wooden bar, what is the bar's smallest diameter?
If we want to make a prism with a wooden base with a 5 cm side of a wooden bar, what is the bar's smallest diameter? - Movement
 From the crossing of two perpendicular roads started two cyclists (each on a different road). One runs at an average speed of 28 km/h, and the second 24 km/h. Determine the distance between them after 45 minutes of cycling.
From the crossing of two perpendicular roads started two cyclists (each on a different road). One runs at an average speed of 28 km/h, and the second 24 km/h. Determine the distance between them after 45 minutes of cycling. - Circumference 46171
 Calculate the circumference and area of a rectangle with one side 6 cm long and a diagonal 10 cm long.
Calculate the circumference and area of a rectangle with one side 6 cm long and a diagonal 10 cm long. - Northeasterly 9681
 A military unit marches in a northerly direction from point A to point B, 15 km away. From place B, it goes 12 km in a northeasterly direction to place C. Determine the direct distance of cities A and C and certainly the deviation -alpha- by which the uni
A military unit marches in a northerly direction from point A to point B, 15 km away. From place B, it goes 12 km in a northeasterly direction to place C. Determine the direct distance of cities A and C and certainly the deviation -alpha- by which the uni - Rhombus
 Internal angles of a rhombus are in ratio 2:3. How many times is the shorter diagonal longer than the side of the rhombus?
Internal angles of a rhombus are in ratio 2:3. How many times is the shorter diagonal longer than the side of the rhombus?
- Simultaneously 82583
 The crane lifts the load in a uniform, straight line to a height of 8 m and simultaneously moves in a horizontal direction to a distance of 6 m. What path did the load cover? What was the resulting velocity of the load if it took 50 seconds to move it
The crane lifts the load in a uniform, straight line to a height of 8 m and simultaneously moves in a horizontal direction to a distance of 6 m. What path did the load cover? What was the resulting velocity of the load if it took 50 seconds to move it - How many
 How many m² of copper sheet is needed to replace the roof of a conical tower with a diameter of 13 meters and a height of 24 meters if we count 8% of the material for bending and waste?
How many m² of copper sheet is needed to replace the roof of a conical tower with a diameter of 13 meters and a height of 24 meters if we count 8% of the material for bending and waste? - Four sided prism
 Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm, and the diagonal body forms a 50-degree angle with the base plane.
Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm, and the diagonal body forms a 50-degree angle with the base plane. - Four-sided 27601
 The house's roof has the shape of a regular four-sided pyramid 4 m high with a base edge of 100 dm. We consider 30% of the roofing in addition to the overlap. Calculate how much m² of roofing is needed to cover the roof.
The house's roof has the shape of a regular four-sided pyramid 4 m high with a base edge of 100 dm. We consider 30% of the roofing in addition to the overlap. Calculate how much m² of roofing is needed to cover the roof. - Company logo
 The company logo consists of a blue circle with a radius of 4 cm and an inscribed white square. What is the area of the blue part of the logo?
The company logo consists of a blue circle with a radius of 4 cm and an inscribed white square. What is the area of the blue part of the logo?
- Circumference 16933
 In the diamond ABCD, the angle BAD is 60°; the length of the diagonal BD is 7 cm. Calculate the circumference of the diamond.
In the diamond ABCD, the angle BAD is 60°; the length of the diagonal BD is 7 cm. Calculate the circumference of the diamond. - Diagonals
 The rhombus has two diagonals, e=14 dm, and f=11 dm. Calculate the side angle and height of the rhombus.
The rhombus has two diagonals, e=14 dm, and f=11 dm. Calculate the side angle and height of the rhombus. - Quadrangular pyramid
 Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =?
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =? - Gardens
 The area of the square garden is 3/4 of the area of the triangular garden with sides of 80 m, 50 m, and 50 m. How many meters of fence do we need to fence a square garden?
The area of the square garden is 3/4 of the area of the triangular garden with sides of 80 m, 50 m, and 50 m. How many meters of fence do we need to fence a square garden? - Dimensions 44081
 In the form of a pyramid on the house with a square floor plan, the roof has dimensions of 12 x 12 m, with a height of 2 m at the highest point. How much roofing do I need to buy? Count on a 10% reserve.
In the form of a pyramid on the house with a square floor plan, the roof has dimensions of 12 x 12 m, with a height of 2 m at the highest point. How much roofing do I need to buy? Count on a 10% reserve.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
