Komplexní čísla kalkulačka
Algebraický tvar:
z = 1,4142136
Fázor (modul a argument):
z = 1,4142136 ∠ 0°
Goniometrický tvar:
z = 1,4142136 × (cos 0° + i sin 0°)
Exponenciálny tvar:
z = 1,4142136 × ei 0 = 1,4142136 × ei 0
Polární souřadnice:
r = |z| = 1,4142136 ... absolutní hodnota (modul)
θ = arg z = 0 rad = 0° = 0π rad ... úhel (argument nebo fáze)
Kartézské souřadnice:
Kartézská forma imaginárního čísla: z = 1,4142136
Reálná část: x = Re z = 1,414
Imaginární část: y = Im z = 0
z = 1,4142136
Fázor (modul a argument):
z = 1,4142136 ∠ 0°
Goniometrický tvar:
z = 1,4142136 × (cos 0° + i sin 0°)
Exponenciálny tvar:
z = 1,4142136 × ei 0 = 1,4142136 × ei 0
Polární souřadnice:
r = |z| = 1,4142136 ... absolutní hodnota (modul)
θ = arg z = 0 rad = 0° = 0π rad ... úhel (argument nebo fáze)
Kartézské souřadnice:
Kartézská forma imaginárního čísla: z = 1,4142136
Reálná část: x = Re z = 1,414
Imaginární část: y = Im z = 0
Kroky výpočtu
- Komplexní číslo: 1-i
- Absolutní hodnota: abs(výsledek kroku č. 1) = abs(1-i) = |(1-i)| = √12 + (-1)2 = 1,4142136
Absolutní hodnota komplexního čísla (nazývaného také modul) je vzdálenost mezi počátkem (nulou) a obrazem komplexního čísla v komplexní rovině. Použitím Pythagorovy věty (Re² + Im² = Abs²) najdeme přeponu pravoúhlého trojúhelníku.
Tato kalkulačka poskytuje služby výpočtu a vyhodnocení výrazů v množině komplexních čísel. Imaginární jednotka je označena jako i nebo j (zejména v elektrotechnice); splňuje rovnici i2 = -1 nebo j2 = -1. Kalkulačka má také konverzi komplexního čísla do goniometrického, exponenciálního tvaru nebo do polárních souřadnic. Zadejte výraz s komplexními čísly, jako například 5*(1+i)(-2-5i)^2
Komplexní čísla ve verzorovom tvaru (polární souřadnice r,θ) zadávejte ve tvaru rLθ např. 5L65, což je totéž jako 5*cis(65°).
Příklad násobení dvou čísel ve verzorovom tvaru: 10L45 * 3L90.
Pro použití ve školství např. výpočtech střídavých proudů na střední odborné škole potřebujete rychlou a jasnou komplexní kalkulačku.
Příklad násobení dvou čísel ve verzorovom tvaru: 10L45 * 3L90.
Pro použití ve školství např. výpočtech střídavých proudů na střední odborné škole potřebujete rychlou a jasnou komplexní kalkulačku.
Základní operace s komplexními čísly
Doufáme, že práce s komplexním číslem je celkem snadná, protože můžete pracovat s pomyslnou jednotkou i jako s proměnnou. A použijte definici i 2 = -1 na zjednodušení složitých výrazů. Mnoho operací je stejných jako operace s dvojrozměrnými vektory.Sčítání
Velmi jednoduché, sečtěte reálné části (bez i) a imaginární části (ty s i):Toto se rovná použití pravidla: (a + b i ) + (c + d i ) = (a + c) + (b + d) i
(1+i) + (6-5i) = 7-4i
12 + 6-5i = 18-5i
(10-5i) + (-5+5i) = 5
Odčítání
Opět velmi jednoduché, odečtěte reálné části a odečtěte imaginární části (ty s i):Toto se rovná použití pravidla: (a + b i ) + (c + d i ) = (a-c) + (b-d) i
(1+i) - (3-5i) = -2+6i
-1/2 - (6-5i) = -6.5+5i
(10-5i) - (-5+5i) = 15-10i
Násobení
Chcete-li vynásobit dvě komplexní čísla, použijte distribuční pravidlo, slučte se dvoučlenné a použijte i 2 = -1 .Toto se rovná použití pravidla: (a + b i ) (c + d i ) = (ac-bd) + (ad + bc) i
(1+i) (3+5i) = 1*3+1*5i+i*3+i*5i = 3+5i+3i-5 = -2+8i
-1/2 * (6-5i) = -3+2.5i
(10-5i) * (-5+5i) = -25+75i
Dělení
Dělení dvou komplexních čísel lze dosáhnout vynásobením čitatele a jmenovatele komplexně sdruženým jmenovatelem. Odstraníme tak imaginární jednotku i ve jmenovateli. Pokud je jmenovatel c + d i , udělejte to bez i (nebo ho udělejte reálným), stačí vynásobit komplexně sdruženým jmenovatelem tj. c-d i :(d + d i) (c-d i ) = c 2 + d 2
c+dia+bi=(c+di)(c−di)(a+bi)(c−di)=c2+d2ac+bd+i(bc−ad)=c2+d2ac+bd+c2+d2bc−adi
(10-5i) / (1+i) = 2.5-7.5i
-3 / (2-i) = -1.2-0.6i
6i / (4+3i) = 0.72+0.96i
Absolutní hodnota nebo modul
Absolutní hodnota nebo modul je vzdálenost obrazu komplexního čísla od počátku v rovině. Kalkulačka používá ke zjištění této vzdálenosti Pythagorovu větu. Velmi jednoduché, viz příklady: |3+4i| = 5|1-i| = 1.4142136
|6i| = 6
abs(2+5i) = 5.3851648
Druhá odmocnina
Druhá odmocnina komplexního čísla (a + bi) je z, jestliže z 2 = (a + bi). Zde končí jednoduchost. Kvůli základní větě algebry budete mít pro dané číslo vždy dvě různé druhé odmocniny. Chcete-li zjistit možné hodnoty, nejjednodušším způsobem je pravděpodobně použít De Moivrove pravidlo (vzorec). Druhá odmocnina není jednoznačně definována funkce pro komplexní číslo. Vypočítáme proto všechny komplexní druhé resp. výše odmocniny (kořeny) z libovolného čísla - dokonce i ve výrazech:sqrt(9i) = 2.1213203+2.1213203i
sqrt(10-6i) = 3.2910412-0.9115656i
pow(-32,1/5)/5 = -0.4
pow(1+2i,1/3)*sqrt(4) = 2.439233+0.9434225i
pow(-5i,1/8)*pow(8,1/3) = 2.3986959-0.4771303i
Druhá mocnina, čtverec, mocnina, komplexní umocňování
Naše kalkulačka dokáže umocňovat jakékoliv komplexní číslo na celé číslo (kladné, záporné), reálné nebo dokonce komplexní číslo. Jinými slovy, vypočítáme "komplexní číslo na komplexní mocninu"Viz příklad:
ii=e−π/2
i^2 = -1i^61 = i
(6-2i)^6 = -22528-59904i
(6-i)^4.5 = 2486.1377428-2284.5557378i
(6-5i)^(-3+32i) = 2929449.0399425-9022199.5826224i
i^i = 0.2078795764
pow(1+i,3) = -2+2i
Funkce
- sqrt
- Druhá odmocnina hodnoty nebo výrazu.
- sin
- sinus hodnoty nebo výrazu. Autodetekce radiánů / stupňů.
- cos
- kosinus hodnoty nebo výrazu. Autodetekce radiánů / stupňů.
- tan / tg
- tangens hodnoty nebo výrazu. Autodetekce radiánů / stupňů.
- exp
- e (Eulerova konstanta) umocněna na výrazu, exponenciála
- pow
- Mocnina jednoho komplexního čísla na jiné celé číslo / reálné / komplexní číslo
- ln
- Přirozený logaritmus hodnoty nebo výrazu
- log
- logaritmus hodnoty nebo výrazu základu-10
- abs nebo | 1 + i |
- Absolutní hodnota hodnoty nebo výrazu
- fáze
- Fáze (úhel) komplexního čísla
- cis
- je méně známá notace: cis (x) = cos (x) + i sin (x); příklad: cis (pi/2) + 3 = 3+i
- conj
- konjugát, sdružené komplexní číslo - příklad: conj(4i+5) = 5-4i
Příklady použití:
• třetí odmocnina: cuberoot(1 - 27i)• odmocniny komplexních čísel: pow(1 + i,1/7)
• fáze, úhel komplexního čísla: phase(1 + i)
• cis tvar komplexní čísla: 5 * cis(45°)
• polární tvar komplexní čísla: 10L60
• Komplexně sdružené číslo: conj(4 + 5i)
• rovnice s komplexními čísly: (z + i/2 )/(1 - i) = 4z + 5i
• soustava rovnic s imaginárními čísly: x - y = 4 + 6i; 3ix + 7y=x + iy
• Moivreova věta - rovnice: z ^ 4=1
• násobení tří komplexních čísel: (1 + 3i)(3 + 4i)(−5 + 3i)
• nájdide součin čísla 3-4i a jemu konjugovaného čísla: (3 - 4i) * conj(3 - 4i)
• operace s komplexními čísly: (3 - i) ^ 3
Zlomky v slovních úlohách:
- Log
 Vypočítej hodnotu výrazu log |3 +7i +5i²| .
Vypočítej hodnotu výrazu log |3 +7i +5i²| . - Tvar
 Určete goniometricky tvar komplexního čísla z = √ 23 -10 i
Určete goniometricky tvar komplexního čísla z = √ 23 -10 i - Vzdálenost komplexních čísel
 Najděte vzdálenost mezi dvěma komplexními čísly: z1=(-8+i) a z2=(-1+i).
Najděte vzdálenost mezi dvěma komplexními čísly: z1=(-8+i) a z2=(-1+i). - Argument a modul
 Najděte mod z a argument z, pokud z=i
Najděte mod z a argument z, pokud z=i - Moivre 2
 Najděte třetí odmocniny z 125(cos 288° + i sin 288°).
Najděte třetí odmocniny z 125(cos 288° + i sin 288°). - Komplexní absolutní hodnota
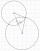 Najděte všechna komplexní řešení (odpověď napište ve tvaru x+iy) soustavy rovnic: {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Najděte všechna komplexní řešení (odpověď napište ve tvaru x+iy) soustavy rovnic: {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8| - Komplexní číslo
 Nechť komplexní číslo z=-√2-√2i, kde i² = -1. Najděte |z|, arg(z), z* (kde * označuje komplexní konjugát) a (1/z). V případě potřeby napište své odpovědi ve tvaru a + i b, kde ai b jsou reálná čísla. Označte polohy čísel z, z* a (1/z) na Argandově diagram
Nechť komplexní číslo z=-√2-√2i, kde i² = -1. Najděte |z|, arg(z), z* (kde * označuje komplexní konjugát) a (1/z). V případě potřeby napište své odpovědi ve tvaru a + i b, kde ai b jsou reálná čísla. Označte polohy čísel z, z* a (1/z) na Argandově diagram
slovní úlohy - více »
