Kombinatorické pravidlo součinu - slovní úlohy a příklady - strana 25 z 29
Počet nalezených příkladů: 566
- Heslo dalibor
Kamila si chce změnit heslo daliborZ tak, že a) dvě souhlásky vymění navzájem mezi sebou, b) změní jednu malou samohlásku na stejnou velkou samohlásku c) udělá obě změny. Kolik možností má na výběr? - Dvojice
Ve třídě je 34 žáků, z toho 14 chlapců a 20 dívek. Kolik dvojic (heterosexuálních, tedy kluk-dívka) můžeme vytvořit? Podle jakého vzorce? - PIN - kódy
Kolik pětimístných PIN - kódů můžeme vytvořit s použitím sudých číslic? - Hokej
V hokejovém zápase padlo 6 gólů. Hráli Česko proti Finsku. Češi vyhráli 4:2. V jakém pořadí mohly padnout góly? Kolik bylo možných průběhů hry? - Trojmístné čísla
Kolik je všech trojmístných čísel z číslic 2 0 4 6 8 (s/bez opakování)? - Pětimístné
Najdi všechna pětimístné čísla, které se dají vytvořit z čísel 12345 tak, aby se čísla neopakovaly a pak také, aby se cisla opakovaly. Uveď i výpočet. - Pravděpodobnost 1775
Firma dosud vyrobila 500 000 aut a z toho 5000 bylo vadných. Jaká je pravděpodobnost, že z denní produkce 50 aut bude nejvíc jedno auto vadné? - Hokej
Zápas v hokeji skončil výsledkem 3:1. Kolik různých průběhů mohl mít daný zápas? - Sklenice
Mám 7 sklenic: 1 2 3 4 5 6 7. Kolik je možnosti postavení sklenic pokud 1 a 2 jsou stále vedle sebe a mohou se navzájem prohodit? - Trojmístné PC
Najdi počet všech trojmístných přirozených čísel, které se dají sestavit z číslic 1,2,3,4 a pro které platí současně ještě tyto podmínky: na místě jednotek je jedna z číslic 1,3,4, na místě stovek číslice 4 nebo 2 - V cukrárně
V cukrárně prodávají 5 druhů zmrzlin. Kolika způsoby si mohu koupit 3 druhy, pokud mi na pořadí zmrzlin nezáleží? - cestovní kancelář
Malá cestovní kancelář nabízí 5 různých zájezdů na líbánky. Jaká je pravděpodobnost, že i nevěsta i ženich zvolí stejný zájezd (předpokládáme, že si vybírají nezávisle)? - Nádoba
V nádobě je 45 bílých a 15 zelených kuliček. Náhodně vybereme 5 kuliček. Jaká je pravděpodobnost, že bude nejvýše jedna zelená? - Trojmístné
Kolik přirozených trojmístných čísel je větších než 321, pokud se žádná číslice v číslech neopakuje? - Předpokládáme 1566
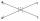V kolika bodech se protíná 9 přímek v rovině, z nichž 4 jsou navzájem rovnoběžné a z ostatních 5 žádné dvě nejsou rovnoběžné (a pokud předpokládáme, že každým průsečíkem procházejí jen dvě přímky)? - Komise - senáty
Rozhodovací komise je tvořena třemi lidmi. Aby bylo rozhodnutí komise plátně, je nutné, aby nejméně dva členové hlasovali stejně. V komisi není možné nehlasovat, každý hlasuje pouze ano nebo ne. Předpokládáme, že první dva členové komise jsou experti a ka - Kamarádi
5 kamarádů šlo do kina. Kolika možnými způsoby se mohou usadit vedle sebe v jedné řadě, pokud jeden z nich chce sedět uprostřed a tím zbylým na místě nezáleží? - Tábor
Na konci tábora si 7 kamarádi navzájem vyměnili adresy. Každý dal zbylým 6 kamarádem svou vizitku. Kolik adres si vyměnili? - Tříciferné čísla
Z číslic 1, 2, 3, 4, 5 utvoř všechna trojmístná čísla tak, aby se v nich neopakovala žádná číslice a aby číslo bylo dělitelné číslem 2. Kolik je takových čísel? - Trojmístne
Kolik je trojmistnych přirozených čísel takových, ze se v nich žádná číslice neopakuje?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám tenhle příklad a my Ti ho zkusíme vypočítat.
