Příklady pro výpočet plošného obsahu tělesa (povrchu tělesa) - strana 24 z 50
Počet nalezených příkladů: 989
- Natření stěn chaty
 Je třeba natřit vnější stěny chaty, jejiž půdorys je obdelník o rozměrech 6,16 m a 8,78 m, vyška stěny chaty je 2,85 m. Chata má pět obdelnikovych oken, tři maji rozměry 1,15 m a 1,32 m a dvě 0,45 m a 0,96 m. Kolik m² je třeba natřit?
Je třeba natřit vnější stěny chaty, jejiž půdorys je obdelník o rozměrech 6,16 m a 8,78 m, vyška stěny chaty je 2,85 m. Chata má pět obdelnikovych oken, tři maji rozměry 1,15 m a 1,32 m a dvě 0,45 m a 0,96 m. Kolik m² je třeba natřit? - Krychle a jehlan
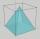 V krychli s délkou hrany 12dm máme vepsaný jehlan s vrcholem ve středu horní stěny kostky. Vypočítejte objem a povrch tohoto jehlanu.
V krychli s délkou hrany 12dm máme vepsaný jehlan s vrcholem ve středu horní stěny kostky. Vypočítejte objem a povrch tohoto jehlanu. - Kužel
 Obsah pláště kužele je 4 cm², obsah podstavy kužele je 2 cm². Určete v stupních úhel (odchylku) strany kužele a roviny podstavy kužele. (Strana kužele je úsečka spojující vrchol kužele s libovolným bodem kružnice podstavy. Všechny strany kužele tvoří pláš
Obsah pláště kužele je 4 cm², obsah podstavy kužele je 2 cm². Určete v stupních úhel (odchylku) strany kužele a roviny podstavy kužele. (Strana kužele je úsečka spojující vrchol kužele s libovolným bodem kružnice podstavy. Všechny strany kužele tvoří pláš - Pravidelného 6566
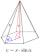 Vypočítejte povrch a objem pravidelného šestibokého jehlanu, jehož podstavná hrana má délku 10 cm a boční hrana délku 26 cm.
Vypočítejte povrch a objem pravidelného šestibokého jehlanu, jehož podstavná hrana má délku 10 cm a boční hrana délku 26 cm. - Pravidelný 6332
 Pravidelný čtyřboký jehlan je vysoký 2m. Výška boční stěny je 2,8m. Jaké rozměry má podstava? Vypočítej povrch a objem jehlanu.
Pravidelný čtyřboký jehlan je vysoký 2m. Výška boční stěny je 2,8m. Jaké rozměry má podstava? Vypočítej povrch a objem jehlanu. - Pravidelného 3162
 Jaký je povrch pravidelného jehlanu se čtvercovou podstavou, pokud každá hrana podstavy měří 40 mm, výška sklonu jehlanu je 44 mm a výška jehlanu je 38 mm?
Jaký je povrch pravidelného jehlanu se čtvercovou podstavou, pokud každá hrana podstavy měří 40 mm, výška sklonu jehlanu je 44 mm a výška jehlanu je 38 mm? - RRT hranol
 Podstava kolmého hranolu je rovnoramenný trojúhelník, jehož základna je 10 cm a rameno 13 cm. Výška hranolu je trojnásobek výšky podstavného trojúhelníku na jeho základnu. Vypočtěte povrch hranolu.
Podstava kolmého hranolu je rovnoramenný trojúhelník, jehož základna je 10 cm a rameno 13 cm. Výška hranolu je trojnásobek výšky podstavného trojúhelníku na jeho základnu. Vypočtěte povrch hranolu. - Připočítat 37871
 Uzavřená lepenková krabice má tvar kvádru o rozměrech 25 cm; 1,2 dm; 0,5m. Kolik lepenky je třeba na zhotovení 20 takových krabic, pokud je třeba připočítat 5 % na zahnutí.
Uzavřená lepenková krabice má tvar kvádru o rozměrech 25 cm; 1,2 dm; 0,5m. Kolik lepenky je třeba na zhotovení 20 takových krabic, pokud je třeba připočítat 5 % na zahnutí. - Rotační kužel 5
 Vypočítejte objem a povrch rotačního kužele o poloměru podstavy r=4,6dm a výškou v=230mm.
Vypočítejte objem a povrch rotačního kužele o poloměru podstavy r=4,6dm a výškou v=230mm. - Počítáme-li 5373
 Kolik m² plechu je potřeba ke zhotovení bedny s víkem, která má tvar kostky s hranou dlouhou 52 cm, počítáme-li 5% na záhyby víka i stěn?
Kolik m² plechu je potřeba ke zhotovení bedny s víkem, která má tvar kostky s hranou dlouhou 52 cm, počítáme-li 5% na záhyby víka i stěn? - Komolý kužel
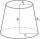 Povrch komolého rotačního kužele S = 7697 m čtverečních, průměry podstav jsou 56m a 42m, určete výška kužele.
Povrch komolého rotačního kužele S = 7697 m čtverečních, průměry podstav jsou 56m a 42m, určete výška kužele. - Akvárium 4
 V akváriu tvaru kvádru s délkou 25 cm a šířkou 30 cm je 9 litrů vody. Vypočítejte obsah ploch, které jsou smáčené vodou.
V akváriu tvaru kvádru s délkou 25 cm a šířkou 30 cm je 9 litrů vody. Vypočítejte obsah ploch, které jsou smáčené vodou. - Spotřebuje 2430
 Skříň má tvar kvádru, jehož přední strana má rozměry 120cm a 150cm, horní stěna 120cm a 60cm. Skříň se venku natírá dvakrát barvou. Kolik barvy se spotřebuje k natírání skříně, když 1kg barvy stačí k natření 8m²?
Skříň má tvar kvádru, jehož přední strana má rozměry 120cm a 150cm, horní stěna 120cm a 60cm. Skříň se venku natírá dvakrát barvou. Kolik barvy se spotřebuje k natírání skříně, když 1kg barvy stačí k natření 8m²? - Trojúhelník 4951
 Vypočítej objem a povrch tělesa, které vznikne tak, že z kvádru o rozměrech 10 cm 15 cm a 20 cm vyřízneme trojboký hranol se stejnou výškou, jehož podstava je pravoúhlý trojúhelník o rozměrech 3 cm , 4 cm a 5 cm
Vypočítej objem a povrch tělesa, které vznikne tak, že z kvádru o rozměrech 10 cm 15 cm a 20 cm vyřízneme trojboký hranol se stejnou výškou, jehož podstava je pravoúhlý trojúhelník o rozměrech 3 cm , 4 cm a 5 cm - Kužel - obal
 Obal tvaru rotačního kužele má objem 1000 cm krychlových a výšku 12 cm. Vypočítejte, kolik plechu potřebujeme na zhotovení tohoto obalu.
Obal tvaru rotačního kužele má objem 1000 cm krychlových a výšku 12 cm. Vypočítejte, kolik plechu potřebujeme na zhotovení tohoto obalu. - Urči povrch
 Urči povrch kužele výšky 30 cm, jehož strana svírá s rovinou podstavy úhel 60°.
Urči povrch kužele výšky 30 cm, jehož strana svírá s rovinou podstavy úhel 60°. - Hrany, poměr
 Délky hran kvádru kvádru jsou v poměru 1:2:3. Vypočítej jejich délku, pokud víte, že povrch celého kvádru je S=5632 m². Proveďte zkoušku správnosti výpočtu.
Délky hran kvádru kvádru jsou v poměru 1:2:3. Vypočítej jejich délku, pokud víte, že povrch celého kvádru je S=5632 m². Proveďte zkoušku správnosti výpočtu. - Obsah 27
 Obsah kvádru: S=376 cm² strany jsou v poměru a: b:c= 3:4:5 vypočítej jeho objem
Obsah kvádru: S=376 cm² strany jsou v poměru a: b:c= 3:4:5 vypočítej jeho objem - Čtyřboký komolý jehlan
 Vypočítejte povrch a objem pravidelného čtyřbokého komolého jehlanu, jsou-li hrany podstavy 87 cm a 64 cm a stěnová výška je 49 cm.
Vypočítejte povrch a objem pravidelného čtyřbokého komolého jehlanu, jsou-li hrany podstavy 87 cm a 64 cm a stěnová výška je 49 cm. - Rotace
 Pravoúhlý trojúhelník má strany a = 11 a b = 10. Přepona je c. Pokud se trojúhelník otáčí kolem strany c jako osa, najděte objem a plochu povrchu kuželové plochy vytvořené touto rotací.
Pravoúhlý trojúhelník má strany a = 11 a b = 10. Přepona je c. Pokud se trojúhelník otáčí kolem strany c jako osa, najděte objem a plochu povrchu kuželové plochy vytvořené touto rotací.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
