Příklady pro výpočet plošného obsahu tělesa (povrchu tělesa) - strana 23 z 50
Počet nalezených příkladů: 989
- Vypočítej 26433
 Vypočítej kolik cm² papíru je třeba koupit na výrobu kostky o rozměrech 60 mm, pokud je třeba na záhyby přidat 12 % navíc.
Vypočítej kolik cm² papíru je třeba koupit na výrobu kostky o rozměrech 60 mm, pokud je třeba na záhyby přidat 12 % navíc. - Hektolitry
 Vypočítejte výšku hranolu, který má povrch 448,88 dm², kde podstavou je čtverec o straně 6,2 dm. Jaký bude objem tělesa v hektolitrech?
Vypočítejte výšku hranolu, který má povrch 448,88 dm², kde podstavou je čtverec o straně 6,2 dm. Jaký bude objem tělesa v hektolitrech? - Pravidelný trojboký
 Pravidelný trojboký hranol, jehož hrany jsou shodné, má povrch 2514 cm² (čtverečních). Urči objem tohoto tělesa v cm³ (l).
Pravidelný trojboký hranol, jehož hrany jsou shodné, má povrch 2514 cm² (čtverečních). Urči objem tohoto tělesa v cm³ (l). - Kostkový cukr
 Kostkový cukr v balení 1 kg je v krabici s rozměry 20 cm, 12 cm a 5 cm. a) Kolik kostek cukru s rozměry 2,5 cm, 2,5 cm a 1 cm se vejde do krabice? b) Vypočítejte hmotnost jedné kostky. c) Kolik čtverečních metrů kartónu je třeba na výrobu 1 000 těchto kra
Kostkový cukr v balení 1 kg je v krabici s rozměry 20 cm, 12 cm a 5 cm. a) Kolik kostek cukru s rozměry 2,5 cm, 2,5 cm a 1 cm se vejde do krabice? b) Vypočítejte hmotnost jedné kostky. c) Kolik čtverečních metrů kartónu je třeba na výrobu 1 000 těchto kra - Sloup
 Vypočítejte objem a povrch podpůrného sloupu tvaru kolmého čtyřbokého hranolu, jehož podstavou je kosočtverec s úhlopříčku u1=102cm, u2=64cm. Výška sloupu je 1,5m.
Vypočítejte objem a povrch podpůrného sloupu tvaru kolmého čtyřbokého hranolu, jehož podstavou je kosočtverec s úhlopříčku u1=102cm, u2=64cm. Výška sloupu je 1,5m. - Kolmý trojboký hranol
 Podstavou kolmého trojbokého hranolu je pravoúhlý trojúhelník s odvěsnami 4,5cm a 6cm. Jaký je povrch tohoto hranolu, pokud je jeho objem 54 cm³?
Podstavou kolmého trojbokého hranolu je pravoúhlý trojúhelník s odvěsnami 4,5cm a 6cm. Jaký je povrch tohoto hranolu, pokud je jeho objem 54 cm³? - Komolý kužel
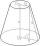 Komolý kužel má poloměr podstav 40cm 10cm a výšku 25cm. Vypočítej jeho povrch a objem.
Komolý kužel má poloměr podstav 40cm 10cm a výšku 25cm. Vypočítej jeho povrch a objem. - Rotační válec 2
 Obvod podstavy rotačního válce je stejně velký, jako je jeho výška. Jaký je povrch válce, když jeho objem je 250 dm³?
Obvod podstavy rotačního válce je stejně velký, jako je jeho výška. Jaký je povrch válce, když jeho objem je 250 dm³? - Kvádr 54
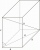 Kvádr má rozměry 15, 20 a 40 cm. Vypočtěte jeho objem a povrch, délku tělesové úhlopříčky a délky všech tří stěnových úhlopříček.
Kvádr má rozměry 15, 20 a 40 cm. Vypočtěte jeho objem a povrch, délku tělesové úhlopříčky a délky všech tří stěnových úhlopříček. - Čtvercového 30191
 Nad pavilonem čtvercového půdorysu se stranou a = 12 m je střecha tvaru jehlanu o výšce 4,5m. Kolik m² plechu je potřeba k zakrytí této střechy?
Nad pavilonem čtvercového půdorysu se stranou a = 12 m je střecha tvaru jehlanu o výšce 4,5m. Kolik m² plechu je potřeba k zakrytí této střechy? - Hodnota S=V
 Určete délku hrany krychle (v centimetrech), která má povrch a objem vyjádřený stejnou číselnou hodnotou. Tuto krychli narýsujte v poměru 1 : 2.
Určete délku hrany krychle (v centimetrech), která má povrch a objem vyjádřený stejnou číselnou hodnotou. Tuto krychli narýsujte v poměru 1 : 2. - Kosočtverec 37443
 Jakou hmotnost má železná tyč 1,5 m dlouhá, jejíž průřez je kosočtverec se stranou a = 45 mm a příslušnou výškou 40 mm? Hustota železa ρ = 7,8 g/cm³? Jaký je povrch železné tyče?
Jakou hmotnost má železná tyč 1,5 m dlouhá, jejíž průřez je kosočtverec se stranou a = 45 mm a příslušnou výškou 40 mm? Hustota železa ρ = 7,8 g/cm³? Jaký je povrch železné tyče? - Vypočítejte 30331
 Vypočítejte množství plechu potřebného na zhotovení uzavřené válcové nádoby o poloměru 2,5 m a výšce 1,2 m, pokud se na spoje a odpad počítá 6%
Vypočítejte množství plechu potřebného na zhotovení uzavřené válcové nádoby o poloměru 2,5 m a výšce 1,2 m, pokud se na spoje a odpad počítá 6% - Trojboký jehlan
 Je dán kolmý pravidelný trojboký jehlan: a=5 cm, v=8 cm, V=28,8 cm³. Jaký je jeho obsah?
Je dán kolmý pravidelný trojboký jehlan: a=5 cm, v=8 cm, V=28,8 cm³. Jaký je jeho obsah? - Hexagon, hexa S,V
 Jaký je povrch a objem pravidelného šestibokého hranolu s hranou podstavy 12cm a výškou hranolu rovnou průměru kružnice opsané podstavě.
Jaký je povrch a objem pravidelného šestibokého hranolu s hranou podstavy 12cm a výškou hranolu rovnou průměru kružnice opsané podstavě. - Stínítko
 Stínítko lampy má být tvořeno pláštěm kužele s průměrem podstavy 48cm a stranou 32cm. Vypočítejte, kolik materiálu bude zapotřebí na jeho zhotovení, počítá-li se s 8% odpadem
Stínítko lampy má být tvořeno pláštěm kužele s průměrem podstavy 48cm a stranou 32cm. Vypočítejte, kolik materiálu bude zapotřebí na jeho zhotovení, počítá-li se s 8% odpadem - Kontejner na odpad
 Pan Milan vyrobil ze dřeva kontejner na tříděný odpad. Z vnější strany se bude malovat. Na okrajích budou oddělení na plasty a papír, uprostřed na sklo. Jak velké plochy bude malovat jednotlivými barvami? Kontejner má tvar kvádru se základnou 1,8 x 0,5 me
Pan Milan vyrobil ze dřeva kontejner na tříděný odpad. Z vnější strany se bude malovat. Na okrajích budou oddělení na plasty a papír, uprostřed na sklo. Jak velké plochy bude malovat jednotlivými barvami? Kontejner má tvar kvádru se základnou 1,8 x 0,5 me - Odchýlka roviny podstavy
 Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°.
Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°. - Krytina
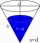 Kolik čtverečních metrů krytiny je potřeba na pokrytí střechy ve tvaru kužele, je-li obvod jeho podstavy 15,7m a výška 30dm
Kolik čtverečních metrů krytiny je potřeba na pokrytí střechy ve tvaru kužele, je-li obvod jeho podstavy 15,7m a výška 30dm - Vodojem - hydroglobus
 Vodojem má tvar koule o průměru 14m. a) Kolik hl vody se do něj vejde? b) Kolik kg barvy je třeba na natření vodojemu, pokud se natírá třikrát a jeden kg barvy vystačí na natření asi 9 m²?
Vodojem má tvar koule o průměru 14m. a) Kolik hl vody se do něj vejde? b) Kolik kg barvy je třeba na natření vodojemu, pokud se natírá třikrát a jeden kg barvy vystačí na natření asi 9 m²?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
