Trojúhelník SV
Kalkulačka používá následující postup řešení: Ze tří dvojích bodů určí Pythagorovou větou délky stran trojúhelníku. Následuje výpočet neznámých parametrů trojúhelníku použitím totožného postupu jako při řešení SSS trojúhelníku.
Trojúhelník v analytických úkolech:
- Těžiště
Vypočítejte souřadnice těžiště T [x, y] trojúhelníku ABC; A[-11,-1] B[25,-2] C[22,-29] - Šipka-vpravo 82083
Trojúhelník má vrcholy na (4, 5), (-3, 2) a (-2, 5). Jaké jsou souřadnice vrcholů obrazu po přeložení (x, y) šipka-vpravo (x + 3, y - 5)? - Jednotkový vektor
Zjistěte jednotkový vektor (jeho souřadnice) k vektoru AB pokud A[-4; 18], B[-12; -13]. - Souřadnice těžiště Souřadnice vrcholů ∆ABC jsou v tomto pořadí (-4, -2), (6, 2) a (4, 6). Najděte těžiště G ∆ABC .
- Vzdálenost
Jaká je vzdálenost mezi počátkem O and bodem A se souřadnicemi [22; 8]? - Těžiště
Těžiště trojúhelníku ABC je v bodě (3,3,3). Pokud jsou souřadnice bodů A a B (3, –5, 7) a (–1, 7, – 6), najděte souřadnice bodu C. @@ - Ortocentrum
Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran. - Souřadnice vektoru
Určete souřadnice vektoru u = CD, pokud C (19; -7) a D (-16; -5) - Těžiště
V trojúhelníku ABC leží bod D[1,-2,6], který je středem strany |BC| a bod G, který je těžištěm trojúhelníku G[8,1,-3]. Najděte souřadnice vrcholu A[x,y,z]. - Souřadnice těžiště
Nechť A = [3, 2, 0], B = [1, -2, 4] a C = [1, 1, 1] jsou 3 body v prostoru. Vypočítejte souřadnice těžiště △ ABC (je to průsečík těžnic). - Trojúhelník 32183
V rovině je dán trojúhelník ABC. A(-3,5), B(2,3), C(-1,-2) zapište souřadnice vektorů u, v, w pokud u=AB, v=AC, w=BC. Zapište souřadnice středů úseček SAB(. .), SAC(. .. ), SBC(. .. ) - Výška lichoběžníku
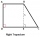Vypočítejte výšku lichoběžníku ABCD, kde jsou souřadnice vrcholů: A [2, 1], B [8, 5], C [5, 5] a D [2, 3] - Koncové body
Koncové body úsečky jsou (-6,1) a (10,11). Jaké jsou souřadnice jejího středu? - Souřadnice vrcholů
Trojúhelník PQR má vrcholy umístěné na souřadnicích (2, 2), (5, -4) a (-4, -1). Jaký typ trojúhelníku je trojúhelník PQR? - Vektor PQ
Ze zadaných souřadnic bodů P = (5, 8) a Q = (6, 9), najděte souřadnice a velikost vektoru PQ.
slovní úlohy - více »
