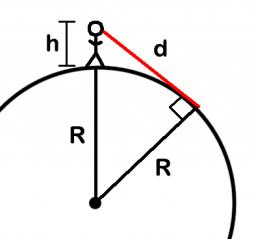
Elevation
What must be an observer's elevation so that he may see an object on the Earth 536 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Horizon
 The top of a lighthouse is 19 m above the sea. How far away is an object just "on the horizon"? [Assume the Earth is a sphere of radius 6378.1 km.]
The top of a lighthouse is 19 m above the sea. How far away is an object just "on the horizon"? [Assume the Earth is a sphere of radius 6378.1 km.] - Earth rotation
 How fast is the place on the Earth's equator moving if the Earth's radius is 6378 km?
How fast is the place on the Earth's equator moving if the Earth's radius is 6378 km? - The spacecraft
 The spacecraft spotted a radar device at an altitude angle alpha = 34 degrees 37 minutes and had a distance of u = 615km from Earth's observation point. Calculate the distance d of the spacecraft from Earth at the moment of observation. Earth is considere
The spacecraft spotted a radar device at an altitude angle alpha = 34 degrees 37 minutes and had a distance of u = 615km from Earth's observation point. Calculate the distance d of the spacecraft from Earth at the moment of observation. Earth is considere - Observer's 82805
 An airliner currently flying over a location 2,400 m away from the observer's location is seen at an elevation angle of 26° 20'. At what height does the plane fly?
An airliner currently flying over a location 2,400 m away from the observer's location is seen at an elevation angle of 26° 20'. At what height does the plane fly?
- Rotation of the Earth
 Calculate the circumferential speed of the Earth's surface at a latitude of 61°. Consider a globe with a radius of 6378 km.
Calculate the circumferential speed of the Earth's surface at a latitude of 61°. Consider a globe with a radius of 6378 km. - Above Earth
 To what height must a boy be raised above the earth to see one-fifth of its surface?
To what height must a boy be raised above the earth to see one-fifth of its surface? - Hot air balloon
 The center of the balloon is at an altitude of 600 m above the ground (AGL). The observer on earth sees the center of the balloon at an elevation angle of 38°20'. The balloon is seen from the perspective of an angle of 1°16'. Calculate the diameter of the
The center of the balloon is at an altitude of 600 m above the ground (AGL). The observer on earth sees the center of the balloon at an elevation angle of 38°20'. The balloon is seen from the perspective of an angle of 1°16'. Calculate the diameter of the - Felix
 Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km.
Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km. - The pond
 We can see the pond at an angle of 65°37'. Its endpoints are 155 m and 177 m away from the observer. What is the width of the pond?
We can see the pond at an angle of 65°37'. Its endpoints are 155 m and 177 m away from the observer. What is the width of the pond?
- Observer 64354
 At what angle of view does an object 70 m long appear to the observer, 50 m away from one end, and 80 m from the other end?
At what angle of view does an object 70 m long appear to the observer, 50 m away from one end, and 80 m from the other end? - Two forces
 Two forces with magnitudes of 25 and 30 pounds act on an object at 10° and 100° angles. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and your final answer.
Two forces with magnitudes of 25 and 30 pounds act on an object at 10° and 100° angles. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and your final answer. - Statue
 On the pedestal, high 4 m is a statue 2.7 m high. At what distance from the statue must the observer stand to see it at the maximum viewing angle? Distance from the eye of the observer from the ground is 1.7 m.
On the pedestal, high 4 m is a statue 2.7 m high. At what distance from the statue must the observer stand to see it at the maximum viewing angle? Distance from the eye of the observer from the ground is 1.7 m. - Moon
 We see Moon in the perspective angle 28'. Moon's radius is 1740 km at the time of the full Moon. Calculate the mean distance of the Moon from the Earth.
We see Moon in the perspective angle 28'. Moon's radius is 1740 km at the time of the full Moon. Calculate the mean distance of the Moon from the Earth. - SSA and geometry
 The distance between the points P and Q was 356 m measured in the terrain. The viewer can see the PQ line at a 107°22' viewing angle. The observer's distance from P is 271 m. Find the viewing angle of P and the observer.
The distance between the points P and Q was 356 m measured in the terrain. The viewer can see the PQ line at a 107°22' viewing angle. The observer's distance from P is 271 m. Find the viewing angle of P and the observer.
- Surveyors
 Surveyors mark 4 points on the globe's surface so their distances are the same. What is their distance from each other?
Surveyors mark 4 points on the globe's surface so their distances are the same. What is their distance from each other? - Storm
 So far, a storm has traveled 35 miles in 1/2 hour in a direction straight to the observer. If it is 5:00 PM, and the storm is 105 miles away from you, at what time will it reach you? Explain how you solved the problem.
So far, a storm has traveled 35 miles in 1/2 hour in a direction straight to the observer. If it is 5:00 PM, and the storm is 105 miles away from you, at what time will it reach you? Explain how you solved the problem. - Chambers
 The decision-making committee consists of three people. For the commission's decision to be valid, at least two members must vote similarly. It is not possible not to vote in the commission. Everyone only votes yes or no. We assume that the first two memb
The decision-making committee consists of three people. For the commission's decision to be valid, at least two members must vote similarly. It is not possible not to vote in the commission. Everyone only votes yes or no. We assume that the first two memb
