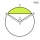
Circular pool
The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool?
Final Answer:

Tips for related online calculators
See also our right triangle calculator.
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticsolid geometryplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- 15-meter-long 2735
 The swimming pool also has a 15-meter-long pool 8 meters wide with a constant depth of 2 meters. If it is always filled 10 cm below the edge, how many hectoliters of water can fit in it?
The swimming pool also has a 15-meter-long pool 8 meters wide with a constant depth of 2 meters. If it is always filled 10 cm below the edge, how many hectoliters of water can fit in it? - Hectoliters 45331
 How many hectoliters of water can fit in a pool with bottom dimensions of 10 m and 20 m and a depth of 4 m?
How many hectoliters of water can fit in a pool with bottom dimensions of 10 m and 20 m and a depth of 4 m? - Hectoliters 48941
 The pool has dimensions: a length of 50 m, a width of 15 m, and a depth of 2 m. It is filled with water to 1/4 of its depth. How many hectoliters of water are in the pool? How many hectoliters of water can fit in a filled pool?
The pool has dimensions: a length of 50 m, a width of 15 m, and a depth of 2 m. It is filled with water to 1/4 of its depth. How many hectoliters of water are in the pool? How many hectoliters of water can fit in a filled pool? - Cylinder horizontally
 The cylinder with a diameter of 3 m and a height/length of 15 m is laid horizontally. Water is poured into it, reaching a height of 60 cm below the cylinder's axis. How many hectoliters of water is in the cylinder?
The cylinder with a diameter of 3 m and a height/length of 15 m is laid horizontally. Water is poured into it, reaching a height of 60 cm below the cylinder's axis. How many hectoliters of water is in the cylinder? - Cross-section 32163
 The bottom of the garden pool of circular cross-section has an inner diameter of d = 4 m. The water depth is 0.8 m. How many liters of water can we fill into the pool?
The bottom of the garden pool of circular cross-section has an inner diameter of d = 4 m. The water depth is 0.8 m. How many liters of water can we fill into the pool? - Water well
 A drilled well has a depth of 20 meters and a radius of 0.1 meters. How many liters of water can fit into the well?
A drilled well has a depth of 20 meters and a radius of 0.1 meters. How many liters of water can fit into the well? - Chord 24
 A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments?
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments?
