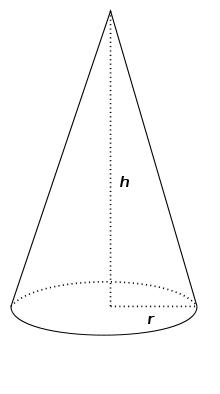
Cone container
The Rotary cone-shaped container has a volume of 1000 cubic cm and a height of 12 cm. Calculate how much metal we need for making this package.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- cone
- surface area
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Rotary cone
 A rotary cone whose height is equal to the circumference of the base has a volume 229 cm³. Calculate the radius of the base circle and the height of the cone.
A rotary cone whose height is equal to the circumference of the base has a volume 229 cm³. Calculate the radius of the base circle and the height of the cone. - Cube-shaped container
 The cube-shaped container has a height of 52 cm and a square base. The container was filled to the brim with water, and then we immersed a metal cube in it, which caused 2.7 l of water to flow out of the container. After removing the cube from the water,
The cube-shaped container has a height of 52 cm and a square base. The container was filled to the brim with water, and then we immersed a metal cube in it, which caused 2.7 l of water to flow out of the container. After removing the cube from the water, - Lamp cone
 Calculate the surface of a lampshade shaped like a rotary truncated cone with a base diameter of 32 cm and 12 cm and a height of 24 cm.
Calculate the surface of a lampshade shaped like a rotary truncated cone with a base diameter of 32 cm and 12 cm and a height of 24 cm. - The cylindrical container
 The cylindrical container has a base area of 300 cm³ and a height of 10 cm. It is 90% filled with water. We gradually insert metal balls into the water, each with a volume of 20 cm³. After inserting how many balls for the first time does water flow over t
The cylindrical container has a base area of 300 cm³ and a height of 10 cm. It is 90% filled with water. We gradually insert metal balls into the water, each with a volume of 20 cm³. After inserting how many balls for the first time does water flow over t
- Consumption 15663
 The cone-shaped sheet metal roof has a base diameter of 80 cm and a height of 60 cm. Calculate the paint consumption for painting this roof if 1 kg of paint is consumed per 6 m² of sheet metal.
The cone-shaped sheet metal roof has a base diameter of 80 cm and a height of 60 cm. Calculate the paint consumption for painting this roof if 1 kg of paint is consumed per 6 m² of sheet metal. - Rotary cone
 The volume of the rotation of the cone is 472 cm³. The angle between the side of the cone and the base angle is 70°. Calculate the lateral surface area of this cone.
The volume of the rotation of the cone is 472 cm³. The angle between the side of the cone and the base angle is 70°. Calculate the lateral surface area of this cone. - Container 15093
 A cone-shaped container with a bottom diameter of 60 cm and a side length of 0.5 m is filled with water. We pour the water into a container with the face of a cylinder with a radius of 3dm and a height of 20cm. Will the cylinder overflow or not be complet
A cone-shaped container with a bottom diameter of 60 cm and a side length of 0.5 m is filled with water. We pour the water into a container with the face of a cylinder with a radius of 3dm and a height of 20cm. Will the cylinder overflow or not be complet - Rotary bodies
 The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area?
The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area? - Block-shaped 37841
 Calculate how much sheet metal is needed to make a closed block-shaped container with dimensions of 2 m, 7 m, and 9 m if we must add 12% to the welds.
Calculate how much sheet metal is needed to make a closed block-shaped container with dimensions of 2 m, 7 m, and 9 m if we must add 12% to the welds.
- Vax candles
 How much dm³ of wax do we need to produce 15 cube-shaped candles with dimensions of 8 cm, 8 cm, and 1 dm?
How much dm³ of wax do we need to produce 15 cube-shaped candles with dimensions of 8 cm, 8 cm, and 1 dm? - The volume
 The volume of the rotating cone is 376.8cm³. The height of this cone is one dm. Calculate the diameter of the cone base.
The volume of the rotating cone is 376.8cm³. The height of this cone is one dm. Calculate the diameter of the cone base. - Identical 32493
 Forty identical traffic cones with base diameter d = 36 cm and height v = 46 cm are to be painted orange on the outside (without base). How much do we pay for paint if we need 500 cm³ of paint to paint 1 m² and 1 liter of paint costs CZK 8?
Forty identical traffic cones with base diameter d = 36 cm and height v = 46 cm are to be painted orange on the outside (without base). How much do we pay for paint if we need 500 cm³ of paint to paint 1 m² and 1 liter of paint costs CZK 8? - Box
 The cardboard is a box-shaped quadrangular prism with a rhombic base. Rhombus has a side 5 cm, one diagonal 8 cm long, and the box's height is 12 cm. The package will open at the top. How many cm² of cardboard do we need to cover overlap and joints that a
The cardboard is a box-shaped quadrangular prism with a rhombic base. Rhombus has a side 5 cm, one diagonal 8 cm long, and the box's height is 12 cm. The package will open at the top. How many cm² of cardboard do we need to cover overlap and joints that a - Surface area
 The volume of a cone is 1000 cm³, and the area of the axis cut is 100 cm². Calculate the surface area of the cone.
The volume of a cone is 1000 cm³, and the area of the axis cut is 100 cm². Calculate the surface area of the cone.
- Lampshade
 The cone-shaped lampshade has a diameter of 30 cm and a height of 10 cm. How many cm² of material will we need when 10% is waste?
The cone-shaped lampshade has a diameter of 30 cm and a height of 10 cm. How many cm² of material will we need when 10% is waste? - Cone-shaped 43291
 Calculate the volume and weight of a pile of cone-shaped sand with a diameter of 8m and a height of v = 4.5m, the density of sand is 1500kg / M cubic
Calculate the volume and weight of a pile of cone-shaped sand with a diameter of 8m and a height of v = 4.5m, the density of sand is 1500kg / M cubic - Cross-section 5089
 The brick pillar with a cross-section of 41x77 cm has a height of 3.25 m. Calculate: (a) the volume of the pillar b) the required number of bricks (if we need 400 pieces per 1 cubic meter)
The brick pillar with a cross-section of 41x77 cm has a height of 3.25 m. Calculate: (a) the volume of the pillar b) the required number of bricks (if we need 400 pieces per 1 cubic meter)
