Examples for secondary school students - page 52 of 213
Number of problems found: 4256
- Transmission 44701
 The electric field performs work 1610 J in the transmission of electric charge of 7 Coulombs between the heating coil terminals. Calculate the voltage between the terminals.
The electric field performs work 1610 J in the transmission of electric charge of 7 Coulombs between the heating coil terminals. Calculate the voltage between the terminals. - Percentage 44691
 How many percent of whipped cream do we make if we mix 41 liters of 38.8% whipped cream and 9 liters of 3.8% milk? (Percent means a percentage of milk fat).
How many percent of whipped cream do we make if we mix 41 liters of 38.8% whipped cream and 9 liters of 3.8% milk? (Percent means a percentage of milk fat). - Remaining 44651
 Jane has to pass ten exams in a year. So far, she has made six and has an average of 2.5. What average must she reach from the remaining tests for her overall average for the year to be 2?
Jane has to pass ten exams in a year. So far, she has made six and has an average of 2.5. What average must she reach from the remaining tests for her overall average for the year to be 2? - Future value investment
 Poseidon deposited 2,747 golden drachmas in a Mount Olympus college savings account to ensure Percy could attend college. It pays 0.04 (percent in decimal form) annual interest. After 11 years, he withdraws the money. How much more money would he have if
Poseidon deposited 2,747 golden drachmas in a Mount Olympus college savings account to ensure Percy could attend college. It pays 0.04 (percent in decimal form) annual interest. After 11 years, he withdraws the money. How much more money would he have if
- Metal balls
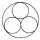 Four metal balls with a diameter of 5 cm are placed in a measuring cylinder with an inner diameter of 10 cm. What is the smallest water volume to be poured into the cylinder so that all balls are below the water level?
Four metal balls with a diameter of 5 cm are placed in a measuring cylinder with an inner diameter of 10 cm. What is the smallest water volume to be poured into the cylinder so that all balls are below the water level? - Truncated pyramid
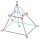 The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base. - Tower's view
 From the church tower's view at the height of 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the height of the house and its distance from the church.
From the church tower's view at the height of 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the height of the house and its distance from the church. - Grams 44441
 How many grams of 70% and 45% acid must be mixed to form 300 grams of 60% acid?
How many grams of 70% and 45% acid must be mixed to form 300 grams of 60% acid? - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
- Measurements: 44341
 Laboratory measurements determined the following roller lengths (in millimeters): {402; 410; 412; 410; 413; 418; 405; 409; 410; 409} Calculate arithmetic, geometric mean, mode, and median.
Laboratory measurements determined the following roller lengths (in millimeters): {402; 410; 412; 410; 413; 418; 405; 409; 410; 409} Calculate arithmetic, geometric mean, mode, and median. - The tetrahedron
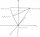 Calculate a regular tetrahedron's surface area and volume 4.9 cm high, and the base edge has a length of 6 cm.
Calculate a regular tetrahedron's surface area and volume 4.9 cm high, and the base edge has a length of 6 cm. - CoG center
 Find the position of the center of gravity of a system of four mass points having masses, m1, m2 = 2 m1, m3 = 3 m1, and m4 = 4 m1, if they lie at the vertices of an isosceles tetrahedron. (in all case
Find the position of the center of gravity of a system of four mass points having masses, m1, m2 = 2 m1, m3 = 3 m1, and m4 = 4 m1, if they lie at the vertices of an isosceles tetrahedron. (in all case - The output
 The output voltage of the transformer is 880 V. The secondary coil has 1200 turns. Transformation ratio k = 4. Find the voltage to which the primary coil is connected. How many turns does the primary coil have if a current of 1 A flows through it? What cu
The output voltage of the transformer is 880 V. The secondary coil has 1200 turns. Transformation ratio k = 4. Find the voltage to which the primary coil is connected. How many turns does the primary coil have if a current of 1 A flows through it? What cu - The transformer
 The transformer's primary coil has 1100 turns and is connected to a voltage of 220 V. How many turns does the secondary coil have when it has a voltage of 55 V? Determine the transformation ratio and decide what the transformation is.
The transformer's primary coil has 1100 turns and is connected to a voltage of 220 V. How many turns does the secondary coil have when it has a voltage of 55 V? Determine the transformation ratio and decide what the transformation is.
- Deceleration
 In a braking test, a vehicle that travels at 51 km/h stops in 5 s. What is its acceleration?
In a braking test, a vehicle that travels at 51 km/h stops in 5 s. What is its acceleration? - The car
 The car weight 1280 kg and increased its speed from 7.3 m/s to 63 km/h on a track of 37.2 m. What force did the car engine have to exert?
The car weight 1280 kg and increased its speed from 7.3 m/s to 63 km/h on a track of 37.2 m. What force did the car engine have to exert? - Arithmetic 44181
 Determine the arithmetic sequence. a3 + a4 = 10 a2 + a5 = 11
Determine the arithmetic sequence. a3 + a4 = 10 a2 + a5 = 11 - Height and base
 An isosceles triangle has an area of 168 cm², and its added height and base are 370 cm. What are the measurements of its height and base?
An isosceles triangle has an area of 168 cm², and its added height and base are 370 cm. What are the measurements of its height and base? - Pyramidal 44061
 A pyramidal candle with a square base has a side edge of s = 12 cm and a base edge of 4 cm. How much wax will we need to make it, and how long is the wick if it is 5% bigger than its height?
A pyramidal candle with a square base has a side edge of s = 12 cm and a base edge of 4 cm. How much wax will we need to make it, and how long is the wick if it is 5% bigger than its height?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
