Harder math problems - page 4 of 5
- Cone in cylinder
 The cylinder is an inscribed cone. Find the ratio of the volume of the cone and cylinder. Please write the ratio as a decimal number and as a percentage.
The cylinder is an inscribed cone. Find the ratio of the volume of the cone and cylinder. Please write the ratio as a decimal number and as a percentage. - One green
 There are 45 white and 15 green balls in the container. We randomly select five balls. What is the probability that there will be one green ball maximally?
There are 45 white and 15 green balls in the container. We randomly select five balls. What is the probability that there will be one green ball maximally? - House roof
 The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m² is needed to cover the roof?
The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m² is needed to cover the roof? - Climb
 The road has climbing 1:28. How big is the angle that corresponds to this climbing?
The road has climbing 1:28. How big is the angle that corresponds to this climbing? - Pizza
 A school survey found that 10 out of 15 students like pizza. If 5 students are chosen randomly, what is the probability that all 5 students like pizza?
A school survey found that 10 out of 15 students like pizza. If 5 students are chosen randomly, what is the probability that all 5 students like pizza? - Cube in a sphere
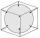 The cube is inscribed in a sphere with a volume 8101 cm³. Determine the length of the edges of a cube.
The cube is inscribed in a sphere with a volume 8101 cm³. Determine the length of the edges of a cube. - IS trapezoid
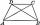 Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm.
Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm. - Tanks
 The fire tank is cuboid in shape, with a rectangular floor measuring 13.3 m × 14.7 m. The water depth is 1.9 m. Water was pumped from the tank into barrels with a capacity of 5 hl. How many barrels would have been used if the water level in the tank
The fire tank is cuboid in shape, with a rectangular floor measuring 13.3 m × 14.7 m. The water depth is 1.9 m. Water was pumped from the tank into barrels with a capacity of 5 hl. How many barrels would have been used if the water level in the tank - Painting school
 Redecoration school had scheduled for four crew to 10 days. After two days, a single worker was ill. For how many days was the school painted when remain workers working with the same tempo?
Redecoration school had scheduled for four crew to 10 days. After two days, a single worker was ill. For how many days was the school painted when remain workers working with the same tempo? - Fertilizer
 Mr. Gherkin uses for fertilization 7% solution of fertilizer. 9 liters of it still left. How much water must be added to the solution to make only the 4% solution?
Mr. Gherkin uses for fertilization 7% solution of fertilizer. 9 liters of it still left. How much water must be added to the solution to make only the 4% solution? - Strawberries
 The father collects strawberries himself in 2 hours and the son in 9 hours. How long will it take them to join him when he comes to help his son collect strawberries after 3 hours?
The father collects strawberries himself in 2 hours and the son in 9 hours. How long will it take them to join him when he comes to help his son collect strawberries after 3 hours? - Euclid1
 The right triangle ABC has hypotenuse c = 20 cm. How large sections cut height hc=9 cm on the hypotenuse c?
The right triangle ABC has hypotenuse c = 20 cm. How large sections cut height hc=9 cm on the hypotenuse c? - Vector sum
 The magnitude of the vector u is 2 and the magnitude of the vector v is 11. The angle between vectors is 64°. What is the magnitude of the vector u + v?
The magnitude of the vector u is 2 and the magnitude of the vector v is 11. The angle between vectors is 64°. What is the magnitude of the vector u + v? - Two doctors
 Doctor A will determine the correct diagnosis with a probability of 89% and doctor B with a probability of 75%. Calculate the probability of proper diagnosis if both doctors diagnose the patient.
Doctor A will determine the correct diagnosis with a probability of 89% and doctor B with a probability of 75%. Calculate the probability of proper diagnosis if both doctors diagnose the patient. - Free fall
 Pavel fall from height 9 m. Calculate the speed at which he hit the ground when falling with acceleration g = 9.81 m/s²
Pavel fall from height 9 m. Calculate the speed at which he hit the ground when falling with acceleration g = 9.81 m/s² - Clock
 What time is now if the time elapsed afternoon is 1/2 of time that elapses before midnight?
What time is now if the time elapsed afternoon is 1/2 of time that elapses before midnight? - Balls
 Three metal balls with volumes V1=12 cm3, V2=112 cm3, and V3=59 cm³ were melted into one ball. Determine its surface area.
Three metal balls with volumes V1=12 cm3, V2=112 cm3, and V3=59 cm³ were melted into one ball. Determine its surface area. - Plastic pipe
 Calculate the plastic pipe's weight with diameter d = 100 mm and length 330 cm if the wall thickness is 4 mm and the density of plastic is 1346 kg/m³.
Calculate the plastic pipe's weight with diameter d = 100 mm and length 330 cm if the wall thickness is 4 mm and the density of plastic is 1346 kg/m³. - Insurance
 The house owner is insured against natural disasters and pays 0.05% annually of the value of the house 88 Eur. Calculate the value of the house. Calculate the probability of disaster if you know that 50% of the insurance is to pay damages.
The house owner is insured against natural disasters and pays 0.05% annually of the value of the house 88 Eur. Calculate the value of the house. Calculate the probability of disaster if you know that 50% of the insurance is to pay damages. - Tiles
 From how many tiles, 20 cm by 30 cm, we can build a square of maximum dimensions if we have a maximum of 275 tiles.
From how many tiles, 20 cm by 30 cm, we can build a square of maximum dimensions if we have a maximum of 275 tiles.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
