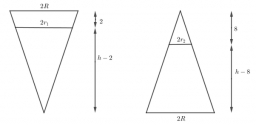
Conical bottle
When a conical bottle rests on its flat base, the water in the bottle is 8 cm from its vertex. When the same conical bottle is turned upside down, the water level is 2 cm from its base. What is the height of the bottle?
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebrasolid geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Equilateral cone
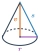 We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down?
We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down? - An experiment
 The three friends agreed to the experiment. At the same time, they all took out an empty cylindrical container on the windowsill and placed it so that it was horizontal. Everyone lives in a different village, and each uses a container with a different bot
The three friends agreed to the experiment. At the same time, they all took out an empty cylindrical container on the windowsill and placed it so that it was horizontal. Everyone lives in a different village, and each uses a container with a different bot - The cylinder base
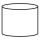 The cylinder with a base of 8 dm² has a volume of 120 liters. From a cylinder filled with water, 40 liters of water were removed. At what height from the bottom /with precision to dm/ is the water level?
The cylinder with a base of 8 dm² has a volume of 120 liters. From a cylinder filled with water, 40 liters of water were removed. At what height from the bottom /with precision to dm/ is the water level? - Jar
 The jar has the shape of a cylinder. Height of jar h = 8 cm, and jar diameter D is 8 cm. After rolling the pot, some water spilled, and the water level accurately reached half of the base. The water level makes a parabola with the same diameter. How to ca
The jar has the shape of a cylinder. Height of jar h = 8 cm, and jar diameter D is 8 cm. After rolling the pot, some water spilled, and the water level accurately reached half of the base. The water level makes a parabola with the same diameter. How to ca - Water 62
 The water tank filled with 1/5 of water is in the shape of a cuboid with a height of 80 cm and a base measuring 30 cm x 40 cm. What is the height of the water level in the tank?
The water tank filled with 1/5 of water is in the shape of a cuboid with a height of 80 cm and a base measuring 30 cm x 40 cm. What is the height of the water level in the tank? - Elevation angle
 A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t - Aquarium
 An aquarium is a rectangular box with a square base containing 62 liters of water. The length of the base edge is 34 cm. To what height does the water level rise?
An aquarium is a rectangular box with a square base containing 62 liters of water. The length of the base edge is 34 cm. To what height does the water level rise?
