Nádoba - kužel
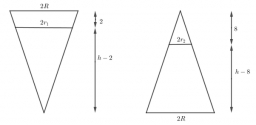
Uzavřená nádoba ve tvaru kužele stojící na své podstavě je naplněna vodou tak, že hladina se nachází 8 cm od vrcholu. Po otočení nádoby o 180 stupňů – stojí na vrcholu – je hladina vzdálena 2 cm od podstavy. Jak vysoká nádoba je?
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Vyzkoušejte naši kalkulačka na přepočet poměru.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte naši kalkulačka na přepočet poměru.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebrastereometrieplanimetriezákladní operace a pojmyJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Nádoba
Nádoba tvaru kvádru má výšku 52 cm a čtvercovou podstavu. Nádoba byla naplněna až po okraj vodou, pak jsme do ní ponořili kovovou kostku, což způsobilo, že z nádoby vyteklo 2,7 l vody. Po vytažení kostky z vody poklesla hladina vody v nádobě o 12 cm. Koli - Nádoba 13
Nádoba ve tvaru válce má obsah podstavy 300cm na druhou a výšku 10 cm. Je naplněna z 90% vodou. Do vody vkládáme postupně kovové kuličky, každou o objemu 20 cm na třetí. Po vložení kolikáté kuličky poprvé přeteče voda přes okraj nádoby? - Nádoba
Nádoba tvaru kostky je naplněna vodou do poloviny své výšky. Pokud dolijeme 20 l vody, bude nádoba naplněna do tří čtvrtin své výšky. Jaký je objem celé nádoby? - Nádoba s vodou
Nádoba tvaru kostky je naplněna do dvou třetin své výšky. Pokud odlijeme 18 litrů, bude naplněna do tří pětin výšky. Jaký je objem celé nádoby? - Válcová 6
Válcová nádoba je ze tří čtvrtin naplněna šesti litry vody. Do nádoby ponoříme těleso tvaru krychle, které klesne ke dnu. Délka hrany krychle je 13 cm. Rozhodni, co se stane s vodou v nádobě po ponoření krychle. - Válec + čtyřstěn
Nádoba tvaru rotačního válce o poloměru podstavy 5 cm je naplněna vodou. O co stoupne hladina vody v nádobě, ponoříme-li do ní pravidelný čtyřstěn o hraně 7 cm. - Uzavřena nádoba
Kolik plechu je třeba na nádobu ve tvaru kvádru svrchu uzavřena), která je 4 m široká, 250 cm dlouhá a 35 dm vysoká? A Kolik litrů vody se do ní vejde?
