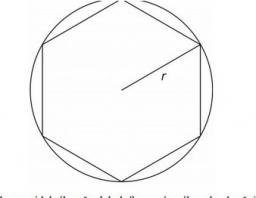
Hexa prism
Determine the volume of the hex prism with a 4 cm edge base and a 28 cm body height.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Calculate 25321
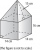 Calculate the body's volume, consisting of a prism and a pyramid with the same square base with an edge of 8 cm. The prism is 20 cm high, and the pyramid is 15 cm.
Calculate the body's volume, consisting of a prism and a pyramid with the same square base with an edge of 8 cm. The prism is 20 cm high, and the pyramid is 15 cm. - Concrete block
 Determine the volume of the concrete block whose one edge of the base is 3 meters long, the body diagonal is 13 meters, and the height is 12 meters.
Determine the volume of the concrete block whose one edge of the base is 3 meters long, the body diagonal is 13 meters, and the height is 12 meters. - Triangular prism
 Calculate the volume and surface area of a triangular prism if it is given: a = 6.8 dm (a = base edge length) ha = 4 dm. (ha = base triangle height length) v = 23 dm (v = body height)
Calculate the volume and surface area of a triangular prism if it is given: a = 6.8 dm (a = base edge length) ha = 4 dm. (ha = base triangle height length) v = 23 dm (v = body height) - Cylinder-shaped 4411
 A cylinder-shaped hole with a diameter of 12 cm is drilled into a block of height 50 cm with a square base with an edge length of 20 cm. The axis of this opening passes through the center of the base of the cuboid. Calculate the volume and surface area of
A cylinder-shaped hole with a diameter of 12 cm is drilled into a block of height 50 cm with a square base with an edge length of 20 cm. The axis of this opening passes through the center of the base of the cuboid. Calculate the volume and surface area of - Perpendicular 79804
 A perpendicular hexagonal prism was created by machining a cube with an edge length of 8 cm. The base of the prism is created from the square wall of the original cube by separating 4 identical right triangles with overhangs of lengths 3cm and 4cm. The he
A perpendicular hexagonal prism was created by machining a cube with an edge length of 8 cm. The base of the prism is created from the square wall of the original cube by separating 4 identical right triangles with overhangs of lengths 3cm and 4cm. The he - Right-angled triangle base
 Find the volume and surface area of a triangular prism with a right-angled triangle base if the length of the prism base legs are 7.2 cm and 4.7 cm and the height of the prism is 24 cm.
Find the volume and surface area of a triangular prism with a right-angled triangle base if the length of the prism base legs are 7.2 cm and 4.7 cm and the height of the prism is 24 cm. - Perpendiculars 2756
 Determine the volume and surface of a prism with the base of a right triangle if the perpendiculars are: a is 1.2 cm. b is 2cm. The height of the body is 0.3 dm.
Determine the volume and surface of a prism with the base of a right triangle if the perpendiculars are: a is 1.2 cm. b is 2cm. The height of the body is 0.3 dm.
