Exponential decay
A tank contains 55 liters of water. Water is flowing out at the rate of 7% per minute. How long does it take to drain the tank?
Result
Result
Showing 3 comments:
Matematik
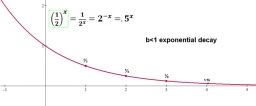
t = infinity time to drain at rate 7% per minute of remaining volume. (exponential decay curve never touch or cross zero - line y=0). Time constant τ = 13.77 min
t2 = 14.286 min if we took 7% as linear volume decay, but this is not correct in this case.
see more on https://en.wikipedia.org/wiki/Exponential_decay
t2 = 14.286 min if we took 7% as linear volume decay, but this is not correct in this case.
see more on https://en.wikipedia.org/wiki/Exponential_decay
Math Student
Thank you so much for your assistance.
I tried to solve using geometric sequence.
At t=~13.77 mins, there's ~20.2 liters of water left in the tank.
I do realize that the exponential function will never be zero. However, logically there must be a finite time when the tank will be emptied.
Still can't resolve the situation.
However, thank you again for your time and effort.
I tried to solve using geometric sequence.
At t=~13.77 mins, there's ~20.2 liters of water left in the tank.
I do realize that the exponential function will never be zero. However, logically there must be a finite time when the tank will be emptied.
Still can't resolve the situation.
However, thank you again for your time and effort.
Matematik
Yes, the right answer is then: the tank is empty in infinity time... T=13.77 mins is time constant, all decays can be normalized in time to have the same curve, but technically emptied at a time approx. 3-5 time constants. After time constant 13.77 mins the tank is on 63%... etc
https://en.wikipedia.org/wiki/Exponential_decay
https://en.wikipedia.org/wiki/Time_constant
https://en.wikipedia.org/wiki/Exponential_decay
https://en.wikipedia.org/wiki/Time_constant
Tips for related online calculators
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Tip: Our volume units converter will help you convert volume units.
Do you want to convert time units like minutes to seconds?
Tip: Our volume units converter will help you convert volume units.
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Water level
To cuboid-shaped poll, bottom size 2m and 3.5m, flows water at a rate of 50 liters per minute. How long will it take for water to reach level 50 cm? - In and out
The empty tank is filled in 12 minutes and empty in 16 minutes. How long does it take to fill if we forget to close the drain? The tank has 1000 liters of volume. - Hectoliters of water
The pool has a total of 126 hectoliters of water. The first pump draws 2.1 liters of water per second. A second pump pumps 3.5 liters of water per second. How long will it take both pumps to drain four-fifths of the water simultaneously? - Minutes 7177
The tank holds 140 liters of water. The tank is filled with a tap in 5 minutes, and the drain is emptied in 7 minutes. How long will it take for the empty tank to fill if we open the faucet and drain? - Water inlets
An Inlet valve with a flow rate of 12 liters per second is filled tank for 72 minutes. How long does it take to fill the full tank if we open one more such valve half an hour after? - Delivers 19143
The pump delivers 34 hl of water per minute. How long does it take to fill the tank with a volume of 10m³? Write the result in hours and minutes. - Delivers 7184 The pump delivers 0.75 hl of water per minute. How long does it take to fill the tank with a volume of 10m³? Write the result in hours and minutes.
- Faucets
A large tank is partially filled with a solution. The tank has a faucet that allows the solution to enter the tank at a rate of 16 3/4 liters per minute. The tank also has a drain that allows the solution to leave the tank at a rate of 19 4/5 liters per m - Efficiency 35023 The cellar, which has a floor area of 50 m2, 3 m below ambient level, was flooded with water to a height of 80 cm. How long does it take for a pump with a power input of 1 kW and an efficiency of 75% (η = 0.75) to drain the water?
- Full of water
From a tank full of water, a man removed 2/7 of it. If it now contains 450 liters, how many liters does it hold when full? - Water reservoir
The water reservoir is filled with one pump for four days by the second one for nine days. An outlet can drain the tank in 12 days. How long does it take to fill the reservoir if both pumps are running and not closed outlet channels? - Water tank
The block-shaped tank is 2.5 m long, 100 cm wide, and 12 dm high. Water flows into the tank at 40 liters per minute. In how many minutes will it be filled with water to two-thirds? - Wood
Wood contains 12% water. One m³ of wood weighs 650 kg. How many liters of water does it contain? - Tank
How many minutes does it take to fill the tank to 25 cubic meters of water filled 150hl per hour? - Volume per time
The length of the cube-shaped tank edge is 4 m. A pump has a capacity of 200 l per minute. How long does fill take for a pump to fill a cube-shaped tank up to 75% of its height? - Volume 6409
The tank has a volume of 1 km cubic. Water flows out of it at a rate of 1 l / s. How long will it be empty? Thank you, we do not know what to do. - Volume 8406
In a minute, 100 l of water flows out of a cube with a volume of 1000 m. How long will it take to empty?
