Two people
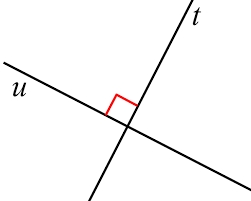
Two straight lines cross at right angles. Two people start simultaneously at the point of intersection. John walks at the rate of 4 kph on one road, and Jenelyn walks at the rate of 8 kph on the other road. How long will it take for them to be 20√5 km apart?
Correct answer:
Showing 1 comment:
Dr Math
checkout also our speed/velocity calculator:
https://www.hackmath.net/en/calculator/conversion-of-speed-units?a=8+kph&submit=Convert&dir=0
https://www.hackmath.net/en/calculator/conversion-of-speed-units?a=8+kph&submit=Convert&dir=0
Tips for related online calculators
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Do you want to convert velocity (speed) units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Do you want to convert velocity (speed) units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- analytic geometry
- line
- vector
- arithmetic
- square root
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Direction vector
 The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lies on the line p C) parametric equations
The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lies on the line p C) parametric equations - Perpendicular lines
 Points A(1,2), B(4,-2) and C(3,-2) are given. Find the parametric equations of the line that: a) It passes through point C and is parallel to the line AB, b) It passes through point C and is perpendicular to line AB.
Points A(1,2), B(4,-2) and C(3,-2) are given. Find the parametric equations of the line that: a) It passes through point C and is parallel to the line AB, b) It passes through point C and is perpendicular to line AB. - Perpendicular and parallel
 Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines?
Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines? - Three points 2
 The three points are A(3, 8), B(6, 2), and C(10, 2). Point D is such that the line DA is perpendicular to AB, and DC is parallel to AB. Calculate the coordinates of D.
The three points are A(3, 8), B(6, 2), and C(10, 2). Point D is such that the line DA is perpendicular to AB, and DC is parallel to AB. Calculate the coordinates of D.
- Collinear lines
 Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC?
Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC? - Line equation:
 Line equation: y-3=8/9(x-5) Solve for slope
Line equation: y-3=8/9(x-5) Solve for slope - The slope 2
 What is the slope of the line that passes through the points (-4, -7) and (-2,-19)? Write your answer in the simplest form.
What is the slope of the line that passes through the points (-4, -7) and (-2,-19)? Write your answer in the simplest form. - Slope of line
 What is the slope of the line that passes through the points: (-2, 4) and (-3, 1)?
What is the slope of the line that passes through the points: (-2, 4) and (-3, 1)? - Divide line segment
 Find the point P on line segment AB, such that |AP| = r |AB|. Coordinates of endpoints: A = (−2, 0, 1), B = (10, 8, 5), ratio r = 1/4.
Find the point P on line segment AB, such that |AP| = r |AB|. Coordinates of endpoints: A = (−2, 0, 1), B = (10, 8, 5), ratio r = 1/4.
- Three
 Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle - Space vectors 3D
 The vectors u = (1; 3; -4), v = (0; 1; 1) are given. Find the size of these vectors, calculate the angle of the vectors, and the distance between the vectors.
The vectors u = (1; 3; -4), v = (0; 1; 1) are given. Find the size of these vectors, calculate the angle of the vectors, and the distance between the vectors. - Perpendicular projection
 Determine the distance of a point B[1, -3] from the perpendicular projection of a point A[3, -2] on a straight line 2 x + y + 1 = 0.
Determine the distance of a point B[1, -3] from the perpendicular projection of a point A[3, -2] on a straight line 2 x + y + 1 = 0. - Place vector
 Place the vector AB if A (3, -1), B (5,3) in point C (1,3) so that AB = CO.
Place the vector AB if A (3, -1), B (5,3) in point C (1,3) so that AB = CO. - Ascend vs. descent
 Which function is growing? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2
Which function is growing? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2
- Three points
 Three points K (-3; 2), L (-1; 4), M (3, -4) are given. Find out: (a) whether the triangle KLM is right b) calculate the length of the line to the k side c) write the coordinates of the vector LM d) write the directional form of the KM side e) write the d
Three points K (-3; 2), L (-1; 4), M (3, -4) are given. Find out: (a) whether the triangle KLM is right b) calculate the length of the line to the k side c) write the coordinates of the vector LM d) write the directional form of the KM side e) write the d - Vector v4
 Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1)
Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1) - Calculate 6
 Calculate the distance of point A[0, 2] from a line passing through points B[9, 5] and C[1, -1].
Calculate the distance of point A[0, 2] from a line passing through points B[9, 5] and C[1, -1].
