Isosceles triangle 9
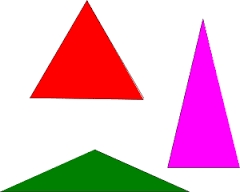
There is an isosceles triangle ABC where AB= AC. The perimeter is 64cm, and the altitude is 24cm. Find the area of the isosceles triangle.
Correct answer:
Showing 2 comments:
Steve
No, your solution starts with h=25cm, but the question says that h=24cm.
So, looking at one-half of the isosceles triangle, x2 + 242 = (32-x)2 solves to x=7cm, which gives the area of the isosceles triangle as 7x24 = 168cm2
So, looking at one-half of the isosceles triangle, x2 + 242 = (32-x)2 solves to x=7cm, which gives the area of the isosceles triangle as 7x24 = 168cm2
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- equation
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- area of a shape
- triangle
- The right triangle altitude theorem
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Richard
 Richard is conducting an experiment. Every time he flips a fair two-sided coin, he also rolls a six-sided die. What is the probability that the coin will land on tails and the die will land on an even number?
Richard is conducting an experiment. Every time he flips a fair two-sided coin, he also rolls a six-sided die. What is the probability that the coin will land on tails and the die will land on an even number? - Locker combination
 Todd forgot the first two numbers of his locker combination. The numbers can be any number 1 through 6. What is the probability that he will guess the first number correctly and the second number incorrectly?
Todd forgot the first two numbers of his locker combination. The numbers can be any number 1 through 6. What is the probability that he will guess the first number correctly and the second number incorrectly? - Multimodal or unimodal
 The weights (in kg) of 13 students of a class are 37,39,33,32,41,33,37,45,43,39, 33,40,39 Find the mode & media of this data (F) Is there more than one mode?
The weights (in kg) of 13 students of a class are 37,39,33,32,41,33,37,45,43,39, 33,40,39 Find the mode & media of this data (F) Is there more than one mode? - Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
- Third tests
 Third periodical tests are 98, 97, 86, 94, 90, 97, 91, and 94. Find the median of her grades and interpret the result.
Third periodical tests are 98, 97, 86, 94, 90, 97, 91, and 94. Find the median of her grades and interpret the result. - The median 2
 Here is a list of numbers: 9.9, 5.9, 3.6, 6.2, 8.9, 0.7, 4.4, 6.7, 9.9, 0.7 State the median. Give your answer as a decimal.
Here is a list of numbers: 9.9, 5.9, 3.6, 6.2, 8.9, 0.7, 4.4, 6.7, 9.9, 0.7 State the median. Give your answer as a decimal. - A population
 A population of fish starts at 8,000 and decreases by 6% per year. Use an exponential function to find the population of fish in 10 years.
A population of fish starts at 8,000 and decreases by 6% per year. Use an exponential function to find the population of fish in 10 years. - The mean 2
 The mean cost of 4 items was $39.96. The first item cost $28.50, the second item cost $41.25, and the third item cost $50. Find the cost of the fourth item.
The mean cost of 4 items was $39.96. The first item cost $28.50, the second item cost $41.25, and the third item cost $50. Find the cost of the fourth item. - Correct mean and CV
 For a group of 100 students, the mean and coefficient of variation of their marks were found to be 60 and 25, respectively. Later, it was found that the scores 45 and 70 were wrongly entered as 40 and 27. Find the corrected mean and coefficient of variati
For a group of 100 students, the mean and coefficient of variation of their marks were found to be 60 and 25, respectively. Later, it was found that the scores 45 and 70 were wrongly entered as 40 and 27. Find the corrected mean and coefficient of variati
- The capacitor
 The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate?
The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate? - IQ scores
 IQ scores are normally distributed with a mean of 100 and a standard deviation of 15. What percentage of the population scores higher than 125 on an IQ test?
IQ scores are normally distributed with a mean of 100 and a standard deviation of 15. What percentage of the population scores higher than 125 on an IQ test? - Isosceles 83157
 Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α. - Sides ratio and angles
 In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC. - The enrolment 2
 The enrolment at a school has increased from 1400 learners to 1600 learners over 5 years. What is the percentage increase in enrolment?
The enrolment at a school has increased from 1400 learners to 1600 learners over 5 years. What is the percentage increase in enrolment?
- Drunken drivers
 40% of drivers driving between 11 pm and 5 am are drunken drivers. In a random sample of 20 drivers driving between 11 pm and 5 am, find the probability that: A) Exactly 12 will be drunken drivers B) At least 7 will be drunken drivers C) At most 5 will be
40% of drivers driving between 11 pm and 5 am are drunken drivers. In a random sample of 20 drivers driving between 11 pm and 5 am, find the probability that: A) Exactly 12 will be drunken drivers B) At least 7 will be drunken drivers C) At most 5 will be - Five couples
 In how many ways can 5 couples arrange themselves in a row if they stay together?
In how many ways can 5 couples arrange themselves in a row if they stay together? - Violin and dance lesson
 Each week, Nina takes a violin lesson and a dance lesson. The dance lesson costs ⅔ as much as the violin lesson, and the combined cost is $75. Which systems of equations could be used to find d, the cost of the dance lesson in dollars, and v, the cost of
Each week, Nina takes a violin lesson and a dance lesson. The dance lesson costs ⅔ as much as the violin lesson, and the combined cost is $75. Which systems of equations could be used to find d, the cost of the dance lesson in dollars, and v, the cost of
