Rhombus
The rhombus with area 137 has one diagonal that is longer by 5 than the second one. Calculate the length of the diagonals and rhombus sides.
Correct answer:

Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
Related math problems and questions:
- Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB. - The perimeter
 The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²?
The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²? - The rectangle 5
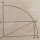 The rectangle OABC has one vertex at O, the center of a circle, and a second vertex A is 2 cm from the edge of the circle, as shown. The vertex A is also a distance of 7 cm from C. The point B and C lie on the circumference of the circle. a. What is the r
The rectangle OABC has one vertex at O, the center of a circle, and a second vertex A is 2 cm from the edge of the circle, as shown. The vertex A is also a distance of 7 cm from C. The point B and C lie on the circumference of the circle. a. What is the r - A rhombus 4
 A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution.
A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution.
- The diagonal 4
 The diagonal of a rhombus measures 16 cm and 30 cm. Find its perimeter.
The diagonal of a rhombus measures 16 cm and 30 cm. Find its perimeter. - Consider 3
 Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid.
Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid. - Rectangular 63094
 Calculate the perimeter and the area of a rectangular garden if the diagonal length is 18 m long and one of the sides of the garden is 9m long.
Calculate the perimeter and the area of a rectangular garden if the diagonal length is 18 m long and one of the sides of the garden is 9m long. - The diagonals
 The diagonals in the diamond ABCD are 6 cm and 8 cm long. What is the perimeter of this diamond?
The diagonals in the diamond ABCD are 6 cm and 8 cm long. What is the perimeter of this diamond? - Side wall planes
 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
- A prism
 A prism with an altitude of 15cm has a base in the form of a regular octagon inscribed in a square of 10cmx10cm. Find the volume of the prism.
A prism with an altitude of 15cm has a base in the form of a regular octagon inscribed in a square of 10cmx10cm. Find the volume of the prism. - Octahedron in a cube
 What largest octahedron can we place inside a cubical box with sides equal to 72?
What largest octahedron can we place inside a cubical box with sides equal to 72? - How long
 How long is the diagonal of the square with side a = 50mm?
How long is the diagonal of the square with side a = 50mm? - Turning machine
 What is the smallest diameter of the cylinder so that a square prism with a side of 40 cm can be turned from it?
What is the smallest diameter of the cylinder so that a square prism with a side of 40 cm can be turned from it? - Trapezoid and diagonals
 Find the area of a trapezoid with bases a = 24 cm, c = 16 cm, and diagonals u = 22 cm, v = 26 cm.
Find the area of a trapezoid with bases a = 24 cm, c = 16 cm, and diagonals u = 22 cm, v = 26 cm.
- The block
 The block has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this block.
The block has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this block. - A paint
 A paint tin is a cylinder of 12cm and a height of 22 cm. Leonardo, the painter, drops his stirring stick into the tin, and it disappears. Work out the maximum length of the stick.
A paint tin is a cylinder of 12cm and a height of 22 cm. Leonardo, the painter, drops his stirring stick into the tin, and it disappears. Work out the maximum length of the stick. - Diagonals of rhombus
 Find the length of the diagonal AC of the rhombus ABCD if its perimeter P = 112 dm and the second diagonal BD has a length of 36 dm.
Find the length of the diagonal AC of the rhombus ABCD if its perimeter P = 112 dm and the second diagonal BD has a length of 36 dm.
