Algebra - math word problems - page 41 of 277
Algebra is a branch of mathematics that uses not only numbers and characters but also letters to solve operations. For example 3x+5x is 8x.Number of problems found: 5536
- Worker salary
 The worker had a salary of CZK 18,000. During the year, his salary was increased by a quarter. He earned a total of CZK 247,500 for the whole year. From which month was his salary increased?
The worker had a salary of CZK 18,000. During the year, his salary was increased by a quarter. He earned a total of CZK 247,500 for the whole year. From which month was his salary increased? - Soccer balls
 Pupils in one class want to buy two soccer balls together. If each of them brings 12.50 euros, they will miss 100 euros; if each brings 16 euros, they will remain 12 euros. How many students are in the class?
Pupils in one class want to buy two soccer balls together. If each of them brings 12.50 euros, they will miss 100 euros; if each brings 16 euros, they will remain 12 euros. How many students are in the class? - Kilometers 29551
 The Poznáváky family traveled by car for 3 days in Slovakia. On the first day, they covered twice as many kilometers as on the second day, and on the third day, they covered 50 kilometers more than on the second day. They drove a total of 700 kilometers i
The Poznáváky family traveled by car for 3 days in Slovakia. On the first day, they covered twice as many kilometers as on the second day, and on the third day, they covered 50 kilometers more than on the second day. They drove a total of 700 kilometers i - Brothers 29471
 The two brothers are 41 years old. One is seven years older than the other. How old is your younger brother?
The two brothers are 41 years old. One is seven years older than the other. How old is your younger brother?
- Three-quarters 29441
 Peter bought a calculator. He saved three-quarters of its price himself, and half of the remaining amount was given to him by his grandfather. He still lacked 7 euros, which he borrowed from his brother. How much did the calculator cost?
Peter bought a calculator. He saved three-quarters of its price himself, and half of the remaining amount was given to him by his grandfather. He still lacked 7 euros, which he borrowed from his brother. How much did the calculator cost? - Sum of seven
 The sum of seven consecutive odd natural numbers is 119. Determine the smallest of them.
The sum of seven consecutive odd natural numbers is 119. Determine the smallest of them. - When I
 When I am as old as my older brother is today, my brother will be twice as old as I am today. a) How old is my brother if I am 8 years old today? b) How old am I if my brother is 21 today?
When I am as old as my older brother is today, my brother will be twice as old as I am today. a) How old is my brother if I am 8 years old today? b) How old am I if my brother is 21 today? - Reservoirs 29051
 The three water reservoirs hold a total of 130 liters. Determine their volumes in m³. If the first fits 15 liters less than the second and 20 liters less than the third.
The three water reservoirs hold a total of 130 liters. Determine their volumes in m³. If the first fits 15 liters less than the second and 20 liters less than the third. - Kindergartens 29031
 We bought 50 kindergartens of two types for the kindergarten - milk for 16 CZK per piece and hazelnuts for 11 CZK per piece. We paid a total of CZK 700. How many chocolates were there?
We bought 50 kindergartens of two types for the kindergarten - milk for 16 CZK per piece and hazelnuts for 11 CZK per piece. We paid a total of CZK 700. How many chocolates were there?
- Collected 28941
 The boys from the science club collected 150 kg of chestnuts in three days for the winter feeding of forest animals. On Monday, they collected 10 kg more than on Tuesday. On Wednesday, after school, they picked two-thirds of the weight of chestnuts they p
The boys from the science club collected 150 kg of chestnuts in three days for the winter feeding of forest animals. On Monday, they collected 10 kg more than on Tuesday. On Wednesday, after school, they picked two-thirds of the weight of chestnuts they p - Forty-eight 28891
 Forty-eight people took part in the tour. Among them were men, women, and children. There were four more women than men and six fewer children than half of the adults. How many men, women, and children took part in the tour?
Forty-eight people took part in the tour. Among them were men, women, and children. There were four more women than men and six fewer children than half of the adults. How many men, women, and children took part in the tour? - Manufacturing 28591
 A furniture manufacturing company consumes 124 cubic meters of spruce and oak lumber per month. Spruce lumber consumes three times more than oak lumber. How much spruce and oak lumber does the company use per month?
A furniture manufacturing company consumes 124 cubic meters of spruce and oak lumber per month. Spruce lumber consumes three times more than oak lumber. How much spruce and oak lumber does the company use per month? - Three-quarters 28581
 Jarek went for a one-day strawberry picking. In the morning, he collected two-fifths of the required amount; in the afternoon, he collected 5 kilograms less than in the morning, and in total, he collected three-quarters of the required amount. How many ki
Jarek went for a one-day strawberry picking. In the morning, he collected two-fifths of the required amount; in the afternoon, he collected 5 kilograms less than in the morning, and in total, he collected three-quarters of the required amount. How many ki - Triple and quadruple rooms
 Up to 48 rooms, some of which are triple and some quadruple, accommodated 173 people so that all beds are occupied. How many triple and how many quadruple rooms were there?
Up to 48 rooms, some of which are triple and some quadruple, accommodated 173 people so that all beds are occupied. How many triple and how many quadruple rooms were there?
- Individual 28401
 In the first and second years, there are 58 pupils in a pile. In the first and third years, there are 57 pupils. In the second and third years, there are 59 pupils. How many students are there: a) In all of them, to the dromedary, b) In individual classes
In the first and second years, there are 58 pupils in a pile. In the first and third years, there are 57 pupils. In the second and third years, there are 59 pupils. How many students are there: a) In all of them, to the dromedary, b) In individual classes - Quarantine cupcakes
 Mr. Honse was baking quarantine cupcakes. Mrs. Carr made twice as many as Mr. Honse. Ms. Sanchez made 12 cupcakes, more than Mr. Honse. If they put all their cupcakes together (which they can't because. of quarantine!), they would have 108 cupcakes. How m
Mr. Honse was baking quarantine cupcakes. Mrs. Carr made twice as many as Mr. Honse. Ms. Sanchez made 12 cupcakes, more than Mr. Honse. If they put all their cupcakes together (which they can't because. of quarantine!), they would have 108 cupcakes. How m - Difference 27431
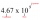 The sum of 2 numbers, x, and y, is 80, and their difference is 16. Determine the numbers x and y.
The sum of 2 numbers, x, and y, is 80, and their difference is 16. Determine the numbers x and y. - Banknotes 27361
 We have the amount of 1,250 euros in banknotes of 100 and 50 euros. We have a total of 17 banknotes. How many are there?
We have the amount of 1,250 euros in banknotes of 100 and 50 euros. We have a total of 17 banknotes. How many are there? - Calculate 27351
 There were goats and chickens in the yard. The number of all heads was 15. The number of all legs was 40. Calculate how many hens there were. Every animal has all its legs.
There were goats and chickens in the yard. The number of all heads was 15. The number of all legs was 40. Calculate how many hens there were. Every animal has all its legs.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
