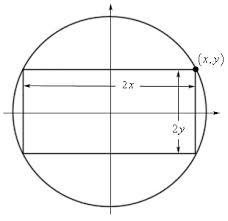
Inscribed rectangle
The circle area is 216. Determine the area of the inscribed rectangle with one side 5 long.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Annular area
 The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area. - Quatrefoil
 Calculate the quatrefoil area, inscribed in a square with a side of 6 cm.
Calculate the quatrefoil area, inscribed in a square with a side of 6 cm. - Infinity
 A square with a side 19 long is an inscribed circle, and the circle is inscribed next square, circle, and so on to infinity. Calculate the sum of the area of all these squares.
A square with a side 19 long is an inscribed circle, and the circle is inscribed next square, circle, and so on to infinity. Calculate the sum of the area of all these squares. - Square inscribed
 Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm.
Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm.
- Vertex of the rectangle
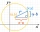 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Circles 2
 Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 16 cm, 20 cm, and 15 cm.
Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 16 cm, 20 cm, and 15 cm. - 6 regular polygon
 A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon.
A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon. - Acreage
 What acreage has a rectangular plot whose diagonal is 34 meters long, and one side has a length of 16 meters? ...
What acreage has a rectangular plot whose diagonal is 34 meters long, and one side has a length of 16 meters? ... - Circular ring
 A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form.
A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form.
- Circumscribed 2671
 The circle's radius circumscribed by the rectangle is 5 cm, and one side of the rectangle is 6 cm long. Calculate the length of the other side and the area of the rectangle.
The circle's radius circumscribed by the rectangle is 5 cm, and one side of the rectangle is 6 cm long. Calculate the length of the other side and the area of the rectangle. - Difference 66354
 A circle is inscribed in a square with a side of 12 cm so that it touches all its sides. Calculate the difference between the area of the square and the circle.
A circle is inscribed in a square with a side of 12 cm so that it touches all its sides. Calculate the difference between the area of the square and the circle. - Square circles
 Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm.
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm. - Folding table
 The folding kitchen table is rectangular with an area of 168dm² (side and is 14 dm long). If necessary, it can be enlarged by sliding two semi-circular plates (at sides b). How much percent will the table area increase? The result round to one-hundredths.
The folding kitchen table is rectangular with an area of 168dm² (side and is 14 dm long). If necessary, it can be enlarged by sliding two semi-circular plates (at sides b). How much percent will the table area increase? The result round to one-hundredths. - Inscribed rectangle
 What is the perimeter of a rectangle inscribed in a circle whose diameter is 5 dm long? Answer: 14 dm
What is the perimeter of a rectangle inscribed in a circle whose diameter is 5 dm long? Answer: 14 dm
- Rectangular 4184
 The rectangular plot has sides 20m and 28m long. Calculate the content of the rhizome and find out how long the longer side of the plot with the same content must be if the shorter side is 16 meters long. Also, calculate the length of the fence around eac
The rectangular plot has sides 20m and 28m long. Calculate the content of the rhizome and find out how long the longer side of the plot with the same content must be if the shorter side is 16 meters long. Also, calculate the length of the fence around eac - Equation of the circle
 Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4].
Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4]. - Circle inscribed
 There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
