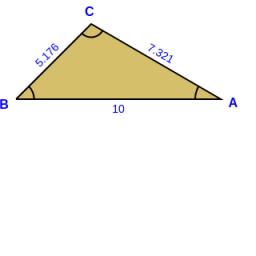
Inner angles
The inner angles of the triangle are 30°, 45°, and 105° and its longest side is 10 cm. Calculate the shortest side length, and write the result in cm up to two decimal places.
Correct answer:
Tips for related online calculators
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Solve 13
 Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a
Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a - A ship
 A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57°
A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° - Triangle 75
 Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1.
Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1. - Designated 71874
 The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started.
The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started.
- Big tower
 From the tower, which is 15 m high and 30 m from the river, the river's width appeared at an angle of 15°. How wide is the river in this place?
From the tower, which is 15 m high and 30 m from the river, the river's width appeared at an angle of 15°. How wide is the river in this place? - Magnitudes 64704
 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Cosine
 Cosine and sine theorem: Calculate all missing values from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm
Cosine and sine theorem: Calculate all missing values from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm - Cosine
 Cosine and sine theorem: Calculate all missing values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
Cosine and sine theorem: Calculate all missing values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? ° - Calculate triangle
 In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm.
In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm.
- Triangle's centroid
 In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t - Aircraft bearing
 Two aircraft will depart from the airport simultaneously. The first flight flies with a course of 30°, and the second with a course of 86°. Both fly at 330 km/h. How far apart will they be in 45 minutes of flight?
Two aircraft will depart from the airport simultaneously. The first flight flies with a course of 30°, and the second with a course of 86°. Both fly at 330 km/h. How far apart will they be in 45 minutes of flight? - Viewing angle
 The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure?
The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure? - The aspect ratio
 The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle.
The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle. - Triangle's 9731
 Solve the triangle ABC if the side a = 52 cm, the height on the other side is vb = 21 cm, and the triangle's area is S = 330 cm².
Solve the triangle ABC if the side a = 52 cm, the height on the other side is vb = 21 cm, and the triangle's area is S = 330 cm².
- Determine 8202
 An observer watches two boats at depth angles of 64° and 48° from the top of the hill, which is 75 m above the lake level. Determine the distance between the boats if both boats and the observer are in the same vertical plane.
An observer watches two boats at depth angles of 64° and 48° from the top of the hill, which is 75 m above the lake level. Determine the distance between the boats if both boats and the observer are in the same vertical plane. - Mast shadow
 The mast has a 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines.
The mast has a 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines. - Children playground
 The playground has a trapezoid shape, and the parallel sides have a length of 36 m and 21 m. The remaining two sides are 14 m long and 16 m long. Find the size of the inner trapezoid angles.
The playground has a trapezoid shape, and the parallel sides have a length of 36 m and 21 m. The remaining two sides are 14 m long and 16 m long. Find the size of the inner trapezoid angles.
