Vnitřní úhly
Vnitřní úhly trojúhelníku mají velikosti 30°, 45°, 105°, jeho nejdelší strana měří 10 cm. Vypočítejte délku nejkratší strany, výsledek uveďte v cm s přesností na dvě desetinná čísla.
Správná odpověď:
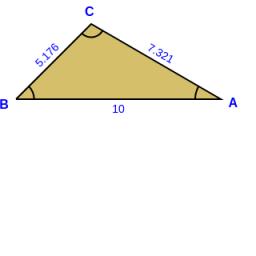
Tipy na související online kalkulačky
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
planimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- 30-60-90
Nejdelší strana trojúhelníku s úhly 30°-60°-90° měří 11. Jaká je délka nejkratší strany? - Rovnoramenný - osy uhlov
V rovnoramenném trojúhelníku ABC se základnou AB platí ∠BAC = 20°, AB = 4. Osa vnitřního úhlu u vrcholu B protíná stranu AC v bodě P. Vypočítejte délku úsečky AP. Výsledek uveďte s přesností na dvě desetinná místa. - Výšky trojúhelníku
Strany trojúhelníku ABC měří 39 cm, 42 cm, 45 cm. Druhá nejdelší výška tohoto trojúhelníku měří 36 cm. Jaká je jeho nejkratší výška? - V trojúhelníku 2
V trojúhelníku XYZ, měří-li úhel X=40° a měří úhel Y=75°. Která strana trojúhelníku je nejdelší a proč? - Ťežišťe a obsah
V trojúhelníku ABC jsou dány délky jeho těžnic tc = 9, ta = 6. Označme T průsečík těžnic, S střed strany BC. Velikost úhlu CTS je 60°. Vypočítejte délku strany BC s přesností na 2 desetinná místa. - Střed přepony
Pro vnitřní úhly trojúhelníku ABC platí, že alfa beta a gama jsou v poměru 1:2:3. Nejdelší strana trojúhelníku AB má délku 30 cm. Vypočítej obvod trojúhelníku CBS, pokud S je střed strany AB. - 36 stupňů
V trojúhelníku měří jeden vnitřní úhel 36 stupňů, druhý úhel je dvakrát větší než úhel třetí. Vypočítejte neznámé úhly.
