Algebra - math word problems - page 263 of 303
Number of problems found: 6048
- Traveling 6067
A car traveling at 75 km/h will drive from place A to place B in 3/4 hours. How long does it take for a cyclist to get there at a speed of 25 km/h? - Introduced 81104
The * (asterisk) operation assigning one number to two pairs of numbers is introduced as follows: (a, b)*(c, d) = ac+bd We know that: (x,2)*(-1, v) = -1 and (2,-1)*(u, v)=5 and (u, v)*(1,1)=-2 What is (1,2)*(x, y) equal to if y=3? - Direction 5122
At 7 o'clock, a truck drove from Olomouc towards Hradec Králové at an average 40 km/h speed. A passenger car left Hradec Králové, 210 km from Olomouc, in 7 hours 45 minutes with an average speed of 80 km/h. At what time and how far from Olomouc will they - Interested 7090
We call a natural number N bombastic if it contains no zero in its notation and if no smaller natural number has the same product of digits as the number N. Charles first became interested in bombastic prime numbers and claimed that there were not many of - Candies
In the confectionery, the price for 1 kg of pistachio candies cost CZK 360, and the price for 1 kg of hazelnut candies was CZK 280. Mixing these two types of sweets created a box of chocolates. How many grams of pistachios and hazelnut candies were in the - Slope
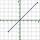What is the slope of the line defined by the equation 4x -2y = 10? - Target
Peter, Martin, and Jirka were a fire in a particular target, with only three fields with values of 12, 18, and 30 points. All boys were firing with the same number of arrows, and all the arrows hit the target, and the results of every two boys differed by - Christmas 7392
The parents won 12,000 euros. They decided to spend 34% of their winnings on Christmas presents and put the rest in the bank. How many euros did they deposit in the bank? What was the annual interest rate at the bank if they were credited with 118.8 euros - Something 5385
Janko got pocket money and wants to buy something good for it. If he purchased four cakes, it would increase by 0.50 euros. If he wanted to buy five cakes, he would miss 0.60 euros. He would spend all his pockets on the rest if he bought two cakes and thr - Divided 71124
We divided line AB into two parts in a ratio of 3:5. The longer part was 6 cm longer than the shorter part. How long was the whole line in cm? - Determine 7314
The hiker went from A to B and back in 3 hours and 41 minutes. The road from A to B is first uphill, then flat, and finally downhill. A hiker walked up a hill at a speed of 4 km/h, on a flat surface at a speed of 5 km/h, and down a hill at a speed of 6 km - Chamber
In the chamber, light is broken, and all from it must be taken at random. Socks have four different colors. If you want to be sure of pulling at least two white socks, we have to bring them out 28 from the chamber. To have such certainty for the pair of g - Self-counting machine
The self-counting machine works exactly like a calculator. The innkeeper wanted to add several three-digit natural numbers on his own. On the first attempt, he got the result in 2224. To check, he added these numbers again, and he got 2198. Therefore, he - Calculation 3620
The mine foreman calculated that 2 pumps must be in operation for 17.5 hours to drain the tunnel. He wanted to speed up the emptying of the shaft and added 3 more identical pumps. How long will it take to empty the shaft? Please also show your calculation - Two trains meet
From A started at 7:15, the express train at a speed of 85 km/h to B. From B, the passenger train started at 8:30 in the direction of A and at a speed of 55 km/h. The distance A and B are 386 1/4 km. At what time and distance do the two trains meet from B - Calculate 2482
The train left Košice at 2:45 PM to Poprad, 120 km away. At 5:45 PM, we met in Poprad with an oncoming train from Žilina, 140 km from Poprad. Calculate what time the train left Žilina if you know that it was 8 km/h faster than the train from Košice. - Complaints
The table is given: days; complaints 0-4; 2 5-9; 4 10-14; 8 15-19; 6 20-24; 4 25-29; 3 30-34; 3 1.1 What percentage of complaints were resolved within two weeks? 1.2 calculate the mean number of days to resolve these complaints. 1.3 calculate the modal nu - Highway tunnel
The company built the highway tunnel from two ends in the north-south direction. The average daily performance of the "northern party" rasters was higher than the average daily power of the "southern party" rasters. After 55 business days, both parties me - Three-digit 5524
Six cards with digits 1, 2, 3, 4, 5, and 6 are on the table. Agnes made a six-digit number from these cards, divisible by six. Then she gradually removed the cards from the right. A five-digit number divisible by five remained on the table when she remove - Electrics - conductor
The wire is 107 meters long at 0 °C, and at every temperature increase of 1 °C, the length increases by 0.15 mm per 1 m length of wire. Determine a function that represents the wire's overall length as a temperature function. What is the length of the wir
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
