Combinatorics - math word problems - page 21 of 54
Number of problems found: 1077
- The big clock
The big clock hands stopped at a random moment. What is the probability that: a) a small hand showed the time between 1:00 and 3:00. b) the big hand was in the same area as a small hand in the role of a)? c) did the hours just show the time between 21:00 - What fraction
What fraction of numbers 1 to 30 is prime? - Probability
A chessboard consists of 8x8 squares forming a square. A rook is unthreatened if there is no other rook in the row and column in which it stands. What is the probability that when 8 rooks are placed on a chessboard, none of them threaten each other (they - Draw a triangle
We have line segments with lengths of 3cm, 5cm, 6cm, 7cm, and 9cm. What is the probability in % that if I randomly select three of them, I will be able to draw a triangle? - Salami
We have six kinds of salami, six of which have ten pieces, and one of which has four pieces. How many ways can we distinctly choose five pieces of salami? - Count of triangles
On each side of an ABCD square is 10 internal points. Determine the number of triangles with vertices at these points. - N points on the side
An equilateral triangle A, B, and C on each of its inner sides lies N=13 points. Find the number of all triangles whose vertices lie at given points on different sides.
- Triangles 8306
Find out how many triangles you create from lines 7 dm, 5 dm, 10 dm, 12 dm, and 15 dm long. - N-gon
How many diagonals have convex 30-gon? - Logik game
Letter game Logik is a two-player game that has the following rules: 1. The first player thinks five-letter word in which no letter is not repeated. 2. The second player writes a five-letter word. 3. The first player answers two numbers. The first number - Permutations with repetitions
How many times can the input of 1.2.2.3.3.3.4 be permutated into four digits, three digits, and two digits without repetition? Ex: 4 digits = 1223, 2213, 3122, 2313, 4321. . etc 3 digits = 122.212.213.432. . etc 2 digits = 12, 21, 31, 23 I have tried the - Training
The table contains the tennis training schedule for Saturday's younger students during the winter indoor season. Before the start of the summer season, preparing a new training schedule, Tomas Kucera will be able to practice only in the morning. Sisters K - STRESSED word
Each letter in STRESSED is printed on identical cards, one letter per card, and assembled in random order. Calculate the probability that the cards spell DESSERTS when assembled. - Win in raffle
The raffle tickets were sold to 200, 5 of which were winning. What is the probability that Peter, who bought one ticket, will win? - Diagonals
What x-gon has 54 diagonals?
- Different 42191
How many different triangles with vertices formed by points A, B, C, D, E, and F can we create? - The spinner
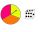The spinner below is spun 12 times. It landed on I 4 times, II 7 times, and III 1 time. What is the difference between the experimental and theoretical probabilities of landing on the II? - Probability 3080
There are eight styles of graduation topics in the Slovak language. The Minister of Education draws 4 of them. How likely is he to choose at least one of the pairs? - Intersection of the lines
How many points do nine lines intersect in a plane, of which four are parallel, and of the other five, no two are parallel (and if we assume that only two lines pass through each intersection)? - Tv dinner tray
I'm trying to calculate the total number of unique potential combinations, but I'm trying to solve for a TV dinner tray with four little sections each: meat, veggie, starch, and dessert. This is more complex because we have different types of meats/veggie
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
Would you like to compute the count of combinations?
