Cone practice problems - page 11 of 13
Number of problems found: 245
- An equilateral cone
Determine the radius and height (in centimeters) of an equilateral cone that has a volume of 1 liter. - Funnel
The funnel has the shape of an equilateral cone. Calculate the surface wetted with water if we poured into the funnel 7.1 liters of water. - Rotating cone
How does the volume of the rotating cone change if: a) double the radius of the base b) We reduce the height three times c) Reduce the radius of the base five times - Frustum of a cone
A reservoir contains 28.54 m³ of water when complete. The diameter of the upper base is 3.5 m, while the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone. - Martians
A sphere-shaped spaceship with a diameter of 6 m landed in the meadow. To avoid attracting attention, the Martians covered it with a roof in the shape of a regular cone. How high will this roof be so that the consumption of roofing is minimal? - Sphere and cone
Within the sphere of radius G = 33 cm, inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone? - Sphere
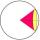Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
- Equilateral 81222
A sphere is inscribed in an equilateral cone with a base diameter of 12 cm. Calculate the volume of both bodies. What percentage of the volume of the cone is filled by the inscribed sphere? - One-quarter 46001
Express in square centimeters the surface of a sphere whose radius is equal to one-quarter of the radius of the cone. The diameter of the base of the cone is 20 cm. - Statements true/false
Which of the statements is not correct: ... - 2x cone
Circular cone height 36 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone. - Surface 64744
The cone is 12 cm high, and the radius of the figure is 9 cm. Find out its surface. - Cutting cone
A cone with a base radius of 10 cm and a height of 12 cm is given. At what height above the base should we divide it by a section parallel to the base so that the volumes of the two resulting bodies are the same? Express the result in cm. - Two vases
Michaela has two vases in her collection. The first vase has the shape of a cone with a base diameter of d = 20 cm; the second vase has the shape of a truncated cone with a lower base of d1 = 25 cm and a diameter of the upper base d2 = 15 cm. Which vase c - The surface
The surface of a truncated rotating cone with side s = 13 cm is S = 510π cm². Find the radii of the bases when their difference in lengths is 10cm.
- A concrete pedestal
A concrete pedestal has the shape of a right circular cone and a height of 2.5 feet. The diameters of the upper and lower bases are 3 feet and 5 feet, respectively. Determine the pedestal's lateral surface area, total surface area, and volume. - The truncated The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm, and height v = 5 cm. What is the volume of the cone from which the truncated cone originated?
- Equilateral cone
We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down? - Frustrum - volume, area
Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm. - Cone - bases The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm.
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
