Equation + third power - practice problems
Number of problems found: 27
- A man 12
 A man in his will shared his money geometrically among his six sons, so the eldest son received ; 5,589 and the youngest son received ; 736. (A)How much will the fourth son receive? (B)How much was shared among them
A man in his will shared his money geometrically among his six sons, so the eldest son received ; 5,589 and the youngest son received ; 736. (A)How much will the fourth son receive? (B)How much was shared among them - Smallest z9
 Find the smallest positive numbers a and b for which 7a³ = 11b⁵
Find the smallest positive numbers a and b for which 7a³ = 11b⁵ - FINDING GEOMETRIC MEANS
 Find the indicated number of geometric means between the pair of numbers. 16 and 81 [insert 3 members: 16, _, _, _, 81]
Find the indicated number of geometric means between the pair of numbers. 16 and 81 [insert 3 members: 16, _, _, _, 81] - Expressed 79474
 The length of the cube's edge in cm is expressed as a natural number. Its volume is greater than 100 and less than 200. Calculate the surface area of the cube.
The length of the cube's edge in cm is expressed as a natural number. Its volume is greater than 100 and less than 200. Calculate the surface area of the cube.
- Smallest 79434
 Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number.
Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number. - Assembling 63964
 Little Pavel was assembling building blocks (a cube is shaped like a cube). He wanted to build a big cube. However, he had 75 dice left, so he increased the edge by one die. Then he was missing 16 dice. How many cubes did he have in the kit?
Little Pavel was assembling building blocks (a cube is shaped like a cube). He wanted to build a big cube. However, he had 75 dice left, so he increased the edge by one die. Then he was missing 16 dice. How many cubes did he have in the kit? - Jointly and cube power
 If y varies jointly as x and the cube of z and y=16 when x=4 and z=2, find an equation representing this relationship. a. y=xz b. y = 2xz³ c.y = 2kx/z³ d.y = xz³/2
If y varies jointly as x and the cube of z and y=16 when x=4 and z=2, find an equation representing this relationship. a. y=xz b. y = 2xz³ c.y = 2kx/z³ d.y = xz³/2 - Find x 2
 Find x, y, and z such that x³+y³+z³=k for each k from 1 to 100. Write down the number of solutions.
Find x, y, and z such that x³+y³+z³=k for each k from 1 to 100. Write down the number of solutions. - Derivative problem
 The sum of two numbers is 12. Find these numbers if: a) The sum of their third powers is minimal. b) The product of one with the cube of the other is maximal. c) Both are positive, and the product of one with the other power of the other is maximal.
The sum of two numbers is 12. Find these numbers if: a) The sum of their third powers is minimal. b) The product of one with the cube of the other is maximal. c) Both are positive, and the product of one with the other power of the other is maximal.
- Magnified cube
 If the lengths of the cube's edges are extended by 5 cm, its volume will increase by 485 cm³. Determine the surface of both the original and the magnified cube.
If the lengths of the cube's edges are extended by 5 cm, its volume will increase by 485 cm³. Determine the surface of both the original and the magnified cube. - Cuboid and ratio
 A cuboid has a volume of 810 cm³. The lengths of edges from the same vertex are in a ratio of 2:3:5. Find the dimensions of a cuboid.
A cuboid has a volume of 810 cm³. The lengths of edges from the same vertex are in a ratio of 2:3:5. Find the dimensions of a cuboid. - One third power
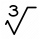 Which equation justifies why ten to the one-third power equals the cube root of ten?
Which equation justifies why ten to the one-third power equals the cube root of ten? - Divide 8
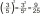 Divide 6840 by x, y, and z in such a way that x has twice as much as y, who has half as much as z
Divide 6840 by x, y, and z in such a way that x has twice as much as y, who has half as much as z - Three members GP
 The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers.
The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers.
- Block-shaped 7976
 A block-shaped pool with a volume of 200m³ is to be built in the recreation area. Its length should be 4 times the width, while the price of 1 m² of the pool bottom is 2 times cheaper than 1 m² of the pool wall. What dimensions must the pool have to make
A block-shaped pool with a volume of 200m³ is to be built in the recreation area. Its length should be 4 times the width, while the price of 1 m² of the pool bottom is 2 times cheaper than 1 m² of the pool wall. What dimensions must the pool have to make - Multiply 6257
 If we multiply the numbers of the last three pages of the book on pyramids, we get the product 23639616. How many pages does the book have if the last page's number is steam?
If we multiply the numbers of the last three pages of the book on pyramids, we get the product 23639616. How many pages does the book have if the last page's number is steam? - Body diagonal
 The cuboid has a volume of 32 cm³. Its side surface area is double as one of the square bases. What is the length of the body diagonal?
The cuboid has a volume of 32 cm³. Its side surface area is double as one of the square bases. What is the length of the body diagonal? - Rectangle pool
 Find dimensions of an open pool with a square bottom with a capacity of 32 m³ to have painted/bricked walls with the least amount of material.
Find dimensions of an open pool with a square bottom with a capacity of 32 m³ to have painted/bricked walls with the least amount of material. - Z9-I-4
 Kate thought of a five-digit integer. She wrote the sum of this number and its half in the first line of the workbook. On the second line, write a total of this number, and its one fifth. She wrote a sum of this number and its one nines on the third row.
Kate thought of a five-digit integer. She wrote the sum of this number and its half in the first line of the workbook. On the second line, write a total of this number, and its one fifth. She wrote a sum of this number and its one nines on the third row.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
