Geometry - math word problems - page 13 of 162
Number of problems found: 3238
- Right-angled triangle
Determine point C so that triangle ABC is right-angled and isosceles with hypotenuse AB, where A[4,-6], B[-2,10] - Chord BC
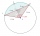A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]? - Similarity of triangles
If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place. - The triangles
The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '. - The triangles
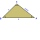Two similar triangles, KLM and ABC, are given. Calculate the lengths of the remaining sides of the triangle KLM. If the lengths of the sides are a = 7 b = 5.6 c = 4.9 k = 5 - Similarity coefficient
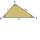The triangles ABC and A'B'C' are similar to the similarity coefficient 2. The sizes of the angles of the triangle ABC are α = 35° and β = 48°. Find the magnitudes of all angles of triangle A'B'C'. - Intersection 6653
Two straight paths cross, making an angle alpha = 53 degrees 30'. There are two pillars on one of them, one at the intersection, the other at a distance of 500m from it. How far does one have to go from the intersection along the other road to see both po - The coordinates 2
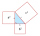The coordinates of the vertices of the triangle shown are A(1,7), B(5,2), and C(5,7). What is the length of segment AB in units? - Medians and sides
Determine the size of a triangle KLM and the size of the medians in the triangle. K=(-5; -6), L=(7; -2), M=(5; 6). - Coordinates 36751
Calculate the circle's length and determine the coordinates of the center of the circle when given its diameter XY, X / -3.2 / and Y / -3, -4 /. - Clock hands
Calculate the internal angles of a triangle whose vertices lie on the clock's 2, 6, and 11 hours. - Vertices of RT
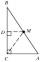Show that the points P1 (5,0), P2 (2,1) & P3 (4,7) are the vertices of a right triangle. - Triangles 6647
For triangles ABC and A'B'C': alpha = alpha with a line, beta with line = beta. a) are these triangles identical? Why? b) are these triangles similar? Why? - Circumscribing
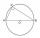Find the radius of the circumscribed circle to the right triangle with legs 6 cm and 3 cm. - What is 10
What is The area of a parallelogram that has vertices with the coordinates (0, 0), (4, 0),(5, 3), and (1, 3)? - Catheti One of the catheti of the right triangle has a length of 12 cm. At what distance from the center of the hypotenuse is another cathetus?
- Circle from string
Martin has a long 628 mm string. He makes a circle from it. Calculate the radius of the circle. - Semicircle
The semicircle with center S and the diameter AB is constructed equilateral triangle SBC. What is the magnitude of the angle ∠SAC? - OK circle
The right triangle has hypotenuse long 33 and one cathetus long 17. Calculate the radius (circumradius) of the circle described. - Add vector
Given that P = (5, 8) and Q = (6, 9), find the component form and magnitude of vector PQ.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
