Geometry - math word problems - page 70 of 162
Number of problems found: 3238
- Tetrahedral pyramid
 Calculate the volume and surface area of a regular tetrahedral pyramid; its height is $b cm, and the length of the edges of the base is 6 cm.
Calculate the volume and surface area of a regular tetrahedral pyramid; its height is $b cm, and the length of the edges of the base is 6 cm. - 3d printer
 3D printing ABS filament with a diameter of 1.75 mm has a density of 1.04 g/cm³. Find the length of m = 5 kg spool filament. (how to calculate length)
3D printing ABS filament with a diameter of 1.75 mm has a density of 1.04 g/cm³. Find the length of m = 5 kg spool filament. (how to calculate length) - Calculate 6207
 The cuboid with a base measuring 17 cm and 13 cm has a surface of 1342 cm². Calculate the height of the cuboid and sketch its network.
The cuboid with a base measuring 17 cm and 13 cm has a surface of 1342 cm². Calculate the height of the cuboid and sketch its network. - Juice-soaked glass
 1. Find the dimensions of a 5-liter cylindrical container if the height of the container is equal to the radius of the base. 2. There are three dl of juice in a cylindrical glass with an inner diameter of 8 cm. Calculate the area of the juice-soaked por
1. Find the dimensions of a 5-liter cylindrical container if the height of the container is equal to the radius of the base. 2. There are three dl of juice in a cylindrical glass with an inner diameter of 8 cm. Calculate the area of the juice-soaked por - A transmitter tower
 A transmitter tower is 80 meters high and is stabilized to the ground by 4 steel cables anchored in the ground 60 meters from the base of the tower. Calculate how many meters of steel cable were needed to stabilize the transmitter tower. The steel cable u
A transmitter tower is 80 meters high and is stabilized to the ground by 4 steel cables anchored in the ground 60 meters from the base of the tower. Calculate how many meters of steel cable were needed to stabilize the transmitter tower. The steel cable u - Insulate house
 The property owner wants to insulate his house. The house has these dimensions of 12, and 12 m is 15 m high. The windows have six dimensions, 170 and 150 cm. Entrance doors are 250 and 170 cm in size. How many square meters of polystyrene does he need?
The property owner wants to insulate his house. The house has these dimensions of 12, and 12 m is 15 m high. The windows have six dimensions, 170 and 150 cm. Entrance doors are 250 and 170 cm in size. How many square meters of polystyrene does he need? - Allan
 Allan keeps tropical fish. His aquarium is 4 feet long, 1 foot wide, and 2 feet tall. Each fish needs at least 0.5ft³ of water. What is the maximum number of fish he can keep in the aquarium? Please show your solution. Please
Allan keeps tropical fish. His aquarium is 4 feet long, 1 foot wide, and 2 feet tall. Each fish needs at least 0.5ft³ of water. What is the maximum number of fish he can keep in the aquarium? Please show your solution. Please - Mine
 In the mine, at depth 18 m is 12°C, and every 50 m, the temperature increases by 1°C. What is the temperature at a depth of 1615 m?
In the mine, at depth 18 m is 12°C, and every 50 m, the temperature increases by 1°C. What is the temperature at a depth of 1615 m? - Dimensions: 27511
 Calculate the surface of the paper cylinder (without lid), which has the following dimensions: bottom radius: 7 cm, cylinder height: 22 cm.
Calculate the surface of the paper cylinder (without lid), which has the following dimensions: bottom radius: 7 cm, cylinder height: 22 cm. - Room dimensions
 The room dimensions are 5m and 3.5m, and the height is 2.85m. Paint the room (even with the ceiling). There will be two layers. Doors and windows have a total of 2.5 m². One box of paint is enough for 6 m². How many boxes of paint are needed? How much do
The room dimensions are 5m and 3.5m, and the height is 2.85m. Paint the room (even with the ceiling). There will be two layers. Doors and windows have a total of 2.5 m². One box of paint is enough for 6 m². How many boxes of paint are needed? How much do - 9-gon pyramid
 Calculate a nine-sided pyramid's volume and surface, the base of which can be inscribed with a circle with radius ρ = 7.2 cm and whose side edge s = 10.9 cm.
Calculate a nine-sided pyramid's volume and surface, the base of which can be inscribed with a circle with radius ρ = 7.2 cm and whose side edge s = 10.9 cm. - Steel tube
 The steel tube has an inner diameter of 4 cm and an outer diameter of 4.8 cm. The density of the steel is 7800 kg/m³. Calculate its length if it weighs 15 kg.
The steel tube has an inner diameter of 4 cm and an outer diameter of 4.8 cm. The density of the steel is 7800 kg/m³. Calculate its length if it weighs 15 kg. - Quadrangular pyramid
 Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =?
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =? - Quadrangular prism
 The quadrangular prism has a volume of 648 cm³. The trapezoid, which is its base, has the dimensions a = 10 cm, c = 5, and height v = 6 cm. What is the height of the prism?
The quadrangular prism has a volume of 648 cm³. The trapezoid, which is its base, has the dimensions a = 10 cm, c = 5, and height v = 6 cm. What is the height of the prism? - Classroom 80652
 The classroom is 11 m long, 6.5 m wide, and 4 m high. I will pay 14.50 for 1 m² of painting. How much will it cost to paint the classroom?
The classroom is 11 m long, 6.5 m wide, and 4 m high. I will pay 14.50 for 1 m² of painting. How much will it cost to paint the classroom? - Cylindrical 66744
 How many liters will fit in a cylindrical container with a base area of 0.06 m² and a height of 5 cm?
How many liters will fit in a cylindrical container with a base area of 0.06 m² and a height of 5 cm? - Dimensions 36001
 The aquarium has the shape of a block with dimensions a = 40cm, b = 15cm, c = 30cm. The aquarium is two-thirds full of water. Calculate the area of wet walls of the aquarium.
The aquarium has the shape of a block with dimensions a = 40cm, b = 15cm, c = 30cm. The aquarium is two-thirds full of water. Calculate the area of wet walls of the aquarium. - Dimensions 31681
 The welded sheet metal tub is shaped a prism with dimensions of 6x2x2 m. How many m³ of water can fit in it, and what is its surface?
The welded sheet metal tub is shaped a prism with dimensions of 6x2x2 m. How many m³ of water can fit in it, and what is its surface? - Calculate 37491
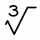 Calculate the edge size of a 48 liter cube.
Calculate the edge size of a 48 liter cube. - Calculate 258
 Calculate the volume and surface area of a prism with a trapezoidal base and a height of 9 cm. The base is an isosceles trapezoid with bases of lengths 3 cm and 6 cm and arms of length 2.5 cm. The height of the base is 2cm.
Calculate the volume and surface area of a prism with a trapezoidal base and a height of 9 cm. The base is an isosceles trapezoid with bases of lengths 3 cm and 6 cm and arms of length 2.5 cm. The height of the base is 2cm.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
