Planimetrics - math word problems - page 47 of 185
Number of problems found: 3686
- Determine 83240
 In triangle ABC, the internal angle beta is twice the size of the angle alpha, and the angle gamma is 20 degrees less than the size of the angle beta. Determine the size of all interior angles of this triangle.
In triangle ABC, the internal angle beta is twice the size of the angle alpha, and the angle gamma is 20 degrees less than the size of the angle beta. Determine the size of all interior angles of this triangle. - Trapezoid 78904
 Calculate the middle crossbar of a trapezoid whose area is 111.8 cm² and height 6.5 cm.
Calculate the middle crossbar of a trapezoid whose area is 111.8 cm² and height 6.5 cm. - Circumference 65674
 The circumference of the triangle is 125 cm. The shortest side is 12 cm shorter than the longest side. The longest side is 7 cm longer than the middle side. How long is the middle side?
The circumference of the triangle is 125 cm. The shortest side is 12 cm shorter than the longest side. The longest side is 7 cm longer than the middle side. How long is the middle side? - Circumference 21603
 The circumference of the diamond is 29.6dm. a - calculate the length of its side b - calculate the area of the diamond if its height measures 5 dm
The circumference of the diamond is 29.6dm. a - calculate the length of its side b - calculate the area of the diamond if its height measures 5 dm - Circumference 19603
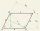 The rhombus has the dimensions a = 9.1 cm; b = 8 cm; height to side a: va = 7.3 cm. Calculate the circumference, area, and size of the second height.
The rhombus has the dimensions a = 9.1 cm; b = 8 cm; height to side a: va = 7.3 cm. Calculate the circumference, area, and size of the second height. - Perpendicular 7712
 Calculate the length of the shadow of a ladder 8 m long leaning against a 6 m high wall. (the sun shines perpendicular to the ladder - see picture).
Calculate the length of the shadow of a ladder 8 m long leaning against a 6 m high wall. (the sun shines perpendicular to the ladder - see picture). - Corresponding 7621
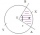 The length of the circular arc at the corresponding angle of 120 ° is 8 cm. What is the size of the whole circle? What is its radius?
The length of the circular arc at the corresponding angle of 120 ° is 8 cm. What is the size of the whole circle? What is its radius? - Circumference 7052
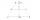 The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem
The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem - Circumference 3170
 Suppose we enlarge the side of the square by half the length, and the circumference of the square increases by 24 cm. Calculate the original side length.
Suppose we enlarge the side of the square by half the length, and the circumference of the square increases by 24 cm. Calculate the original side length. - A triangle 4
 A triangle has a perimeter of 18a + 6b + 15 and has sides of lengths 5a + 7 and 8a +4b. What is the length of the third side? Write an expression and simplify it to find the solution to the problem.
A triangle has a perimeter of 18a + 6b + 15 and has sides of lengths 5a + 7 and 8a +4b. What is the length of the third side? Write an expression and simplify it to find the solution to the problem. - Interior angles - sum
 For the sum s of the interior angles of a polygon, where n is the number of its sides, the relation s=(n−2)⋅180 degrees applies. How many sides does a polygon have if the sum of its interior angles is 900°?
For the sum s of the interior angles of a polygon, where n is the number of its sides, the relation s=(n−2)⋅180 degrees applies. How many sides does a polygon have if the sum of its interior angles is 900°? - Circular segment
 What is the radius of a circular section whose central angle is 36° and the area of S = 53.095 cm²?
What is the radius of a circular section whose central angle is 36° and the area of S = 53.095 cm²? - An equilateral
 An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle?
An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle? - Rectangular trapezoid
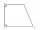 In a rectangular trapezoid ABCD with right angles at vertices A and D with sides a = 12cm, b = 13cm, c = 7cm. Find the angles beta and gamma and height v.
In a rectangular trapezoid ABCD with right angles at vertices A and D with sides a = 12cm, b = 13cm, c = 7cm. Find the angles beta and gamma and height v. - Rectangular garden 2
 A farmer bought 600 m of wire for the fence. He wants to use it to besiege a rectangular garden with a surface of 16875 m². Calculate the size of the garden.
A farmer bought 600 m of wire for the fence. He wants to use it to besiege a rectangular garden with a surface of 16875 m². Calculate the size of the garden. - RT sides
 Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm.
Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm. - Castle windows
 Seven twelfth windows in the castle are in the shape of an n-gon. Six-fourteenths of these windows are quadrangular in shape, while two-ninths of them are square windows. How many windows are there in the castle if there are 15 square windows?
Seven twelfth windows in the castle are in the shape of an n-gon. Six-fourteenths of these windows are quadrangular in shape, while two-ninths of them are square windows. How many windows are there in the castle if there are 15 square windows? - Pavement
 Calculate the length of the pavement that runs through a circular square with a diameter of 40 m if the distance of the pavement from the center is 15 m.
Calculate the length of the pavement that runs through a circular square with a diameter of 40 m if the distance of the pavement from the center is 15 m. - Circle annulus
 There are two concentric circles in the figure. The chord of the larger circle, 10 cm long, is tangent to the smaller circle. What does annulus have?
There are two concentric circles in the figure. The chord of the larger circle, 10 cm long, is tangent to the smaller circle. What does annulus have? - Bike wheel
 The bike wheel has a radius of 30cm. How often does it turn if we go on a 471m bike?
The bike wheel has a radius of 30cm. How often does it turn if we go on a 471m bike?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
