Pythagorean theorem - math word problems - page 15 of 73
Number of problems found: 1449
- Medians of isosceles triangle
The isosceles triangle has a base ABC |AB| = 16 cm and a 10 cm long arm. What is the length of the medians? - Park
In the park is a marked diamond-shaped line connecting locations A, D, S, C, B, and A. Calculate its length if |AB| = 108 m, |AC| = 172.8 m. - Drainage channel
The drainage channel's cross-section is an isosceles trapezoid whose bases are 1.80 m and 0.90 m long, and the arm is 0.60 meters long. Calculate the channel's depth. - Diamond
The side length of the diamond is 35 cm, and the length of the diagonal is 56 cm. Calculate the height and length of the second diagonal. - RT 10
The area of the right triangle is 15 cm², and one of its catheti is a=7 cm. Calculate the perimeter of the triangle ABC. - Column
The vertical pole high 7 m tall broke, and its toe fell 4.7 m from the bottom of the pole. At what height above the ground does the pole break? - Without Euclid laws
Right triangle ABC with a right angle at the C has a=5 and hypotenuse c=22. Calculate the height h of this triangle without the use of Euclidean laws. - Triangle and its heights
Calculate the length of the sides of the triangle ABC if va=13 cm, vb=15 cm and side b are 5 cm shorter than side a. - Right isosceles
Calculate the area of the isosceles right triangle whose perimeter is 26 cm. - Square diagonal
Calculate the length of the diagonal of the square with side a = 11 cm. - R triangle
Calculate the right triangle area whose longer leg is 7 dm shorter than the hypotenuse and 10 dm longer than the shorter leg. - Common chord
Two circles with radii 18 cm and 20 cm intersect at two points. Its common chord is long 11 cm. What is the distance of the centers of these circles? - Against 82851
A 3.4 m long ladder is leaning against a wall. Its lower end is 1.6 m away from the wall. At what height does the ladder touch the wall? - Determine 82595 A ladder is 7 meters long and is leaning against a wall so that its lower end is 4 meters away from the wall. Determine how high the ladder reaches
- Circumference 82552
The isosceles trapezoid has a base length of 12 cm, a height of 4.5 cm, and a height of 5 cm. What is its circumference? - Circle and chord
The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc? - Arithmetic 80808
The lengths of the sides of a right triangle form the first 3 terms of the arithmetic sequence. Its area is 6 cm². Find length of its sides. - Constructed 77874
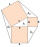Squares are constructed above the overhangs and the transom. Connecting the outer vertices of adjacent squares creates three triangles. Prove that their areas are the same. - Perimeter 7882
The diagonals of the diamond are 2.4 dm and 1.8 dm long. What is the perimeter of this diamond? - Perimeter 6254
Perimeter and area of the rectangle. Diagonal 260m and one side 150m
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
