Pythagorean theorem - math word problems - page 41 of 73
Number of problems found: 1446
- A man 7
A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles toward N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.) - Equilateral triangle ABC
In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl - Points on circle
The Cartesian coordinate system with the origin O is a sketched circle k /center O; radius r=2 cm/. Write all the points that lie on a circle k and whose coordinates are integers. Write all the points on the circle I with center O and radius r=5 cm, whose - Perpendicular 62844
A body with a mass of 4 kg hits an obstacle at a speed of 10 m/s. After the collision, the body continued to move at a speed of 6 m/s, while the direction of this speed was perpendicular to the direction of the speed before the collision. Find: a) change - Rectangular trapezoid
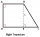The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters - Forces
Forces with magnitudes F1 = 42N and F2 = 35N act at a common point and make an angle of 77°12'. How big is their resultant? - Crossroads
A passenger car and an ambulance come to the rectangular crossroads, and the ambulance leaves. The passenger car is moving at 39 km/h, and the ambulance is moving at 41 km/h. Calculate the relative speed of the ambulance moving to the car. - Equation of the circle
Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4]. - Find all
Find all right-angled triangles whose side lengths form an arithmetic sequence. - Meridian ground speed
The plane flies south at an average speed of 190 km/h, and the wind blows from west to east at a speed of 20 m/s. How fast and in what direction (relative to the meridian) will the plane move relative to the ground? - The bomber
An aircraft flying at an altitude of 1260 m. From what distance in front of the target must a parachute load be dropped from an airplane? The load slopes at a speed of 5.6 m/s and moves in the direction of movement at 12 m/s. What is the direct distance o - Climb
The road sign that informs the climb is 10.3%—the car drives 10 km along this road. What is the height difference that the car went? - An observer
An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower? - Circles
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Tunnel - quadrilateral
How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral. - Construct 8
Construct an analytical geometry problem where it is asked to find the vertices of a triangle ABC: The vertices of this triangle are points A (1,7), B (-5,1) C (5, -11). The said problem should be used the concepts of distance from a point to a line, rati - Right-angled triangle
The right-angled triangle XYZ is similar to the triangle ABC, which has a right angle at the vertex X. The following applies: side a = 9 cm, x=4 cm, x = v-4 (v = height of triangle ABC). Calculate the unknown side lengths of both triangles. - Circle described
The circle radius described in the right triangle with a 6 cm long leg is 5 cm. Calculate the circumference of this triangle. - Distance
What is the distance between the origin and the point (-11; 13)? - Airplane navigation
An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 35.95°W. How far is the plane from the airport (round to the nearest mile)?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
