Pythagorean theorem - math word problems - page 42 of 73
Number of problems found: 1450
- Circle described
 The circle radius described in the right triangle with a 6 cm long leg is 5 cm. Calculate the circumference of this triangle.
The circle radius described in the right triangle with a 6 cm long leg is 5 cm. Calculate the circumference of this triangle. - Airplane navigation
 An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 35.95°W. How far is the plane from the airport (round to the nearest mile)?
An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 35.95°W. How far is the plane from the airport (round to the nearest mile)? - Angle ASB
 On a circle with a radius of 10 cm and with a center S, the points A, B, and C are given so that the central angle ASB is 60 degrees and the central angle ASC is 90 degrees. Find the length of the circular arc and the amount of AB and AC offsets.
On a circle with a radius of 10 cm and with a center S, the points A, B, and C are given so that the central angle ASB is 60 degrees and the central angle ASC is 90 degrees. Find the length of the circular arc and the amount of AB and AC offsets. - A cell tower
 A cell tower is located at coordinates (-5, -7) and has a circular range of 12 units. If Mr. XYZ is located at coordinates (4,5), will he be able to get a signal?
A cell tower is located at coordinates (-5, -7) and has a circular range of 12 units. If Mr. XYZ is located at coordinates (4,5), will he be able to get a signal? - Resultant force
 Calculate mathematically and graphically the resultant of three forces with a common center if: F1 = 50 kN α1 = 30° F2 = 40 kN α2 = 45° F3 = 40 kN α3 = 25°
Calculate mathematically and graphically the resultant of three forces with a common center if: F1 = 50 kN α1 = 30° F2 = 40 kN α2 = 45° F3 = 40 kN α3 = 25° - Polygon 3
 Polygon ABCD is dilated, rotated, and translated to form polygon QWER. The endpoints A and B are at (0, -7) and (8, 8), and the endpoints QW are at (6, -6) and (2, 1.5). What is the scale factor of the dilation?
Polygon ABCD is dilated, rotated, and translated to form polygon QWER. The endpoints A and B are at (0, -7) and (8, 8), and the endpoints QW are at (6, -6) and (2, 1.5). What is the scale factor of the dilation? - Lunes of Hippocrates
 Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the - X-coordinate 81737
 In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right.
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right. - Intersection 74914
 Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis.
Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis. - Two chords
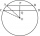 Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords.
Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords. - Triangle ABC
 There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr
There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr - Right-angled 80745
 The area of a right-angled triangle KLM with a right angle at the vertex L is 60 mm square, and its hypotenuse k is 10 mm long. Triangles KLM and RST are similar. The similarity ratio is k=2.5. Calculate the area of triangle RST.
The area of a right-angled triangle KLM with a right angle at the vertex L is 60 mm square, and its hypotenuse k is 10 mm long. Triangles KLM and RST are similar. The similarity ratio is k=2.5. Calculate the area of triangle RST. - Ellipse
 Ellipse is expressed by equation 9x² + 25y² - 54x - 100y - 44 = 0. Find the length of primary and secondary axes, eccentricity, and coordinates of the ellipse's center.
Ellipse is expressed by equation 9x² + 25y² - 54x - 100y - 44 = 0. Find the length of primary and secondary axes, eccentricity, and coordinates of the ellipse's center. - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Two chords
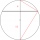 Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center.
Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center. - Rectangular trapezoid
 The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid.
The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid. - Quadrilateral - irregular
 Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees
Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees - Calculate 6706
 Given a triangle KLM points K [-3.2] L [7, -3] M [8.5]. Calculate the side lengths and perimeter.
Given a triangle KLM points K [-3.2] L [7, -3] M [8.5]. Calculate the side lengths and perimeter. - Isosceles 6673
 Isosceles triangle X'Y'Z' . It is similar to triangle XYZ. The base of triangle XYZ has length |XY|=4cm. The size of the angle at the X vertex is 45 degrees. Draw a triangle X'Y'Z' whose base is 8 cm long.
Isosceles triangle X'Y'Z' . It is similar to triangle XYZ. The base of triangle XYZ has length |XY|=4cm. The size of the angle at the X vertex is 45 degrees. Draw a triangle X'Y'Z' whose base is 8 cm long. - 3 positive charges
 Three equal positive charges Q are located at the vertices of an isosceles right triangle ABC. The right angle is at vertex A. The length of side AB is 1m. What is the electric field strength at the center S of side BC, i.e., what force would act on a pos
Three equal positive charges Q are located at the vertices of an isosceles right triangle ABC. The right angle is at vertex A. The length of side AB is 1m. What is the electric field strength at the center S of side BC, i.e., what force would act on a pos
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
