Pythagorean theorem - math word problems - page 43 of 73
Number of problems found: 1453
- Segment length
 Calculate the length of the line segment AB, given A [8; -6] and B [4; 2]
Calculate the length of the line segment AB, given A [8; -6] and B [4; 2] - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Triangle point coordinates
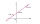 In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right.
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right. - Triangle perimeter function
 Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis.
Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis. - Luiza
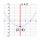 Luiza delivers newspapers in her neighborhood. If you plot the points (-1, 1), (4, 1), (4, -2), and (-1, -2), you will create a representation of the route she takes in miles. How many miles does her route cover?
Luiza delivers newspapers in her neighborhood. If you plot the points (-1, 1), (4, 1), (4, -2), and (-1, -2), you will create a representation of the route she takes in miles. How many miles does her route cover? - Drawing Similar Triangle
 Isosceles triangle X'Y'Z' . It is similar to triangle XYZ. The base of triangle XYZ has length |XY|=4cm. The size of the angle at the X vertex is 45 degrees. Draw a triangle X'Y'Z' whose base is 8 cm long.
Isosceles triangle X'Y'Z' . It is similar to triangle XYZ. The base of triangle XYZ has length |XY|=4cm. The size of the angle at the X vertex is 45 degrees. Draw a triangle X'Y'Z' whose base is 8 cm long. - Area of iso-trap
 Find the area of an isosceles trapezoid if the lengths of its bases are 16 cm and 30 cm and the diagonals are perpendicular to each other.
Find the area of an isosceles trapezoid if the lengths of its bases are 16 cm and 30 cm and the diagonals are perpendicular to each other. - Mass point
 Two equal forces of 30 Newtons act on a mass point. Find the magnitude of the resultant force if these forces form an angle of 42°.
Two equal forces of 30 Newtons act on a mass point. Find the magnitude of the resultant force if these forces form an angle of 42°. - Triangle height measurement
 Draw an isosceles triangle ABC with a base 7 cm long and shoulders 5.5 cm long. Assemble all the heights, measure them, and calculate their sum.
Draw an isosceles triangle ABC with a base 7 cm long and shoulders 5.5 cm long. Assemble all the heights, measure them, and calculate their sum. - Forces on earth directions
 A force of 60 N [North] and 80 N [East] is exerted on an object weight of 10 kg. What is the acceleration of the object?
A force of 60 N [North] and 80 N [East] is exerted on an object weight of 10 kg. What is the acceleration of the object? - Circular segment
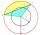 Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Railways
 Railways climb 2.8 ‰. Calculate the height difference between two points on the railway distant 5997 meters.
Railways climb 2.8 ‰. Calculate the height difference between two points on the railway distant 5997 meters. - Ellipse
 Ellipse is expressed by equation 9x² + 25y² - 54x - 100y - 44 = 0. Find the length of primary and secondary axes, eccentricity, and coordinates of the ellipse's center.
Ellipse is expressed by equation 9x² + 25y² - 54x - 100y - 44 = 0. Find the length of primary and secondary axes, eccentricity, and coordinates of the ellipse's center. - Vector endpoint magnitude
 The endpoint of the vector, which is located at the origin of the Cartesian system Oxy, is given. Determine the coordinates of the vector and its magnitude, and sketch it: P[3,4]; Q[-2,7]; S[-5,-2] . .. i.e., Vectors PO, QO, SO
The endpoint of the vector, which is located at the origin of the Cartesian system Oxy, is given. Determine the coordinates of the vector and its magnitude, and sketch it: P[3,4]; Q[-2,7]; S[-5,-2] . .. i.e., Vectors PO, QO, SO - Three vertices
 The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A.
The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A. - Axial symmetry
 Find the image A' of point A [1,2] in axial symmetry with the axis p: x = -1 + 3t, y = -2 + t (t = are a real number)
Find the image A' of point A [1,2] in axial symmetry with the axis p: x = -1 + 3t, y = -2 + t (t = are a real number) - Prove
 Prove that k1 and k2 are the equations of two circles. Find the equation of the line that passes through the centers of these circles. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0
Prove that k1 and k2 are the equations of two circles. Find the equation of the line that passes through the centers of these circles. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0 - Triangle construction sides
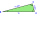 Sestroj triangle HOP, if o = 6 cm, h = 8 cm and | PHO | = 90 °
Sestroj triangle HOP, if o = 6 cm, h = 8 cm and | PHO | = 90 ° - Angle between vectors
 Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21)
Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21) - Isosceles triangle
 In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C.
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
