Pythagorean theorem - math word problems - page 44 of 73
Number of problems found: 1451
- Railways
 Railways climb 2.8 ‰. Calculate the height difference between two points on the railway distant 5997 meters.
Railways climb 2.8 ‰. Calculate the height difference between two points on the railway distant 5997 meters. - Determine 82478
 Determine the equation of the parabola that has the point F = [3,2] as its focus and the line x+y+1=0 as its shift line.
Determine the equation of the parabola that has the point F = [3,2] as its focus and the line x+y+1=0 as its shift line. - Angle between vectors
 Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21)
Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21) - Lengths of medians from coordinates
 There is a triangle ABC: A [-6.6; 1.2], B [3.4; -5.6], C [2.8; 4.2]. Calculate the lengths of its medians.
There is a triangle ABC: A [-6.6; 1.2], B [3.4; -5.6], C [2.8; 4.2]. Calculate the lengths of its medians. - Mass point
 Two equal forces of 30 Newtons act on a mass point. Find the magnitude of the resultant force if these forces form an angle of 42°.
Two equal forces of 30 Newtons act on a mass point. Find the magnitude of the resultant force if these forces form an angle of 42°. - Axial symmetry
 Find the image A' of point A [1,2] in axial symmetry with the axis p: x = -1 + 3t, y = -2 + t (t = are a real number)
Find the image A' of point A [1,2] in axial symmetry with the axis p: x = -1 + 3t, y = -2 + t (t = are a real number) - Forces on earth directions
 A force of 60 N [North] and 80 N [East] is exerted on an object weight of 10 kg. What is the acceleration of the object?
A force of 60 N [North] and 80 N [East] is exerted on an object weight of 10 kg. What is the acceleration of the object? - Distance
 What is the distance between the origin and the point (-11; 13)?
What is the distance between the origin and the point (-11; 13)? - Square
 Points A[9,9] and B[-4,1] are adjacent vertices of the square ABCD. Calculate the area of the square ABCD.
Points A[9,9] and B[-4,1] are adjacent vertices of the square ABCD. Calculate the area of the square ABCD. - Determine 82394
 Determine the equation of the circle that passes through the point M(-1,2) and N( 3,0) and whose center lies on the line p: x=-3+t, y=-1+t,
Determine the equation of the circle that passes through the point M(-1,2) and N( 3,0) and whose center lies on the line p: x=-3+t, y=-1+t, - Three vertices
 The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A.
The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A. - Calculate 8
 Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0.
Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0. - Quadrilateral 2
 Show that the quadrilateral with vertices A(0,1), B(4,2), C(3,6) D(-5,4) has two right triangles.
Show that the quadrilateral with vertices A(0,1), B(4,2), C(3,6) D(-5,4) has two right triangles. - Circular segment
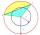 Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Circle
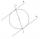 The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0
The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0 - Equilateral 35073
 Draw an equilateral triangle ABC with a side of 8.5 cm. Assemble all the mines and measure them. What is the difference between the longest and the shortest of them?
Draw an equilateral triangle ABC with a side of 8.5 cm. Assemble all the mines and measure them. What is the difference between the longest and the shortest of them? - Three parallels
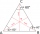 The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle.
The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle. - On line
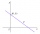 On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0].
On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0]. - Construct 80719
 Construct a rectangle ABCD if a = 8cm and the length of the diagonal AC is 13cm. Measure the length of the sides of the rectangle.
Construct a rectangle ABCD if a = 8cm and the length of the diagonal AC is 13cm. Measure the length of the sides of the rectangle. - Triangle 67504
 Sestroj triangle HOP, if o = 6 cm, h = 8 cm and | PHO | = 90 °
Sestroj triangle HOP, if o = 6 cm, h = 8 cm and | PHO | = 90 °
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
