Right triangle + surface area - practice problems
Number of problems found: 279
- A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - Rotating 28501
 Which bags shaped like the shell of a rotating cone can hold the most popcorn? The first bag has a height of 20 cm, and the length of its side is 24 cm. The second bag has a base radius of 10 cm and a height of 25 cm.
Which bags shaped like the shell of a rotating cone can hold the most popcorn? The first bag has a height of 20 cm, and the length of its side is 24 cm. The second bag has a base radius of 10 cm and a height of 25 cm. - Side wall planes
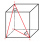 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Triangular prism
 The base of the perpendicular triangular prism is a rectangular triangle with a hypotenuse of 10 cm and one leg of 8 cm. The prism height is 75% of the perimeter of the base. Calculate the volume and surface of the prism.
The base of the perpendicular triangular prism is a rectangular triangle with a hypotenuse of 10 cm and one leg of 8 cm. The prism height is 75% of the perimeter of the base. Calculate the volume and surface of the prism.
- Calculate 82409
 The lamp shade should be formed by the shell of a cone with a base diameter of 48 cm and a side of 32 cm. Calculate how much material will be needed to make it, assuming 8% waste
The lamp shade should be formed by the shell of a cone with a base diameter of 48 cm and a side of 32 cm. Calculate how much material will be needed to make it, assuming 8% waste - Tetrahedral pyramid
 Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'.
Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'. - Right triangular prism
 We have a cuboid with a base and dimensions of 12 cm and 5 cm and a height of 4 cm. The tablecloth is cut into two identical triangular prisms with right triangular bases. We painted the surface of the created prisms with color. Calculate the surface area
We have a cuboid with a base and dimensions of 12 cm and 5 cm and a height of 4 cm. The tablecloth is cut into two identical triangular prisms with right triangular bases. We painted the surface of the created prisms with color. Calculate the surface area - Base diagonal
 In a regular 4-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the surface area and volume of the pyramid.
In a regular 4-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the surface area and volume of the pyramid. - Rotary bodies
 The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area?
The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area?
- Cone side
 Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side.
Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side. - Conical area
 A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation.
A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation. - Church roof
 The roof of the church tower has the shape of a regular tetrahedral pyramid with a base edge length of 5.4 meters and a height of 5 m. It was found that the 27% covering of the roof area needs to be corrected. What amount of material will be required?
The roof of the church tower has the shape of a regular tetrahedral pyramid with a base edge length of 5.4 meters and a height of 5 m. It was found that the 27% covering of the roof area needs to be corrected. What amount of material will be required? - Martians
 A sphere-shaped spaceship with a diameter of 6 m landed in the meadow. To avoid attracting attention, the Martians covered it with a roof in the shape of a regular cone. How high will this roof be so that the consumption of roofing is minimal?
A sphere-shaped spaceship with a diameter of 6 m landed in the meadow. To avoid attracting attention, the Martians covered it with a roof in the shape of a regular cone. How high will this roof be so that the consumption of roofing is minimal? - Ratio-cuboid
 The lengths of the edges of the cuboid are in the ratio 2: 3: 6. Its body diagonal is 14 cm long. Calculate the volume and surface area of the cuboid.
The lengths of the edges of the cuboid are in the ratio 2: 3: 6. Its body diagonal is 14 cm long. Calculate the volume and surface area of the cuboid.
- Cone container
 The Rotary cone-shaped container has a volume of 1000 cubic cm and a height of 12 cm. Calculate how much metal we need for making this package.
The Rotary cone-shaped container has a volume of 1000 cubic cm and a height of 12 cm. Calculate how much metal we need for making this package. - Prism
 The base of a vertical triangular prism is a right triangle with legs 4.5 cm and 6 cm long. What is the surface of the prism if its volume is 54 cubic centimeters?
The base of a vertical triangular prism is a right triangle with legs 4.5 cm and 6 cm long. What is the surface of the prism if its volume is 54 cubic centimeters? - Pyramid in cube
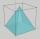 In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid.
In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid. - Triangular pyramid
 It is given perpendicular regular triangular pyramid: base side a = 5 cm, height v = 8 cm, volume V = 28.8 cm³. What is its area (surface area)?
It is given perpendicular regular triangular pyramid: base side a = 5 cm, height v = 8 cm, volume V = 28.8 cm³. What is its area (surface area)? - Tropics and polar zones
 What percentage of the Earth's surface lies in the tropical, temperate, and polar zone? Tropics border individual zones at 23°27' and polar circles at 66°33'.
What percentage of the Earth's surface lies in the tropical, temperate, and polar zone? Tropics border individual zones at 23°27' and polar circles at 66°33'.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
