Solid geometry, stereometry - page 105 of 121
Number of problems found: 2409
- Cuboid Dimensions Ratio Surface
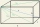 The base of a cuboid is a rectangle. The ratio of its length to width is 3:2. The length of the rectangle of the base is in the ratio of 4:5 to the height of the block. The sum of the lengths of all the edges of the block is 2.8m. Find: a) the surface of
The base of a cuboid is a rectangle. The ratio of its length to width is 3:2. The length of the rectangle of the base is in the ratio of 4:5 to the height of the block. The sum of the lengths of all the edges of the block is 2.8m. Find: a) the surface of - Vintner
 How high can a vintner fill the keg with crushed red grapes if these grapes occupy a volume of 20 percent? The keg is cylindrical with a diameter of the base of 1 m and a volume of 9.42 hl. Start from the premise that says that fermentation will fill the
How high can a vintner fill the keg with crushed red grapes if these grapes occupy a volume of 20 percent? The keg is cylindrical with a diameter of the base of 1 m and a volume of 9.42 hl. Start from the premise that says that fermentation will fill the - Hip-roof
 The roof consists of two isosceles trapezoids and two isosceles triangles. The roof plan is a rectangle with dimensions of 8m and 14m, and the roof ridge is 8m long. The height of the trapezoid is 5m, the height of the triangles is 4.2m. How many tiles ar
The roof consists of two isosceles trapezoids and two isosceles triangles. The roof plan is a rectangle with dimensions of 8m and 14m, and the roof ridge is 8m long. The height of the trapezoid is 5m, the height of the triangles is 4.2m. How many tiles ar - Box cardboard material
 The closed box has the shape of a perpendicular prism with the base of an equilateral triangle. The edge of the base is 24 cm long, and the height of the box is 0.5 m. Calculate how many square meters of cardboard are needed to make 20 such boxes, assumin
The closed box has the shape of a perpendicular prism with the base of an equilateral triangle. The edge of the base is 24 cm long, and the height of the box is 0.5 m. Calculate how many square meters of cardboard are needed to make 20 such boxes, assumin - A cylinder
 A cylinder 108 cm high has a circumference of 24 cm. A string makes exactly six complete turns around the cylinder while its two ends touch the top and bottom. (forming a spiral around the cylinder). How long is the string in cm?
A cylinder 108 cm high has a circumference of 24 cm. A string makes exactly six complete turns around the cylinder while its two ends touch the top and bottom. (forming a spiral around the cylinder). How long is the string in cm? - The conical roof
 The conical roof above the warehouse has a diameter of the lower part (base) d = 11.2 m and a height v = 3.3 m. How many rectangular steel plates with dimensions of 1.4 m and 0.9 m were needed to produce this roof if the seams and waste required an increa
The conical roof above the warehouse has a diameter of the lower part (base) d = 11.2 m and a height v = 3.3 m. How many rectangular steel plates with dimensions of 1.4 m and 0.9 m were needed to produce this roof if the seams and waste required an increa - The cone
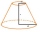 The cone has a base radius of 12 cm and a height of 20 cm. It was truncated at 6 cm from the base. We created a truncated cone - frustum. Find the radius of the base of the truncated cone.
The cone has a base radius of 12 cm and a height of 20 cm. It was truncated at 6 cm from the base. We created a truncated cone - frustum. Find the radius of the base of the truncated cone. - Painting
 To paint the pool with dimensions: 2 meters depth, 3m x 4m we bought paint to 50 meters square. How much "paint" will be wasted?
To paint the pool with dimensions: 2 meters depth, 3m x 4m we bought paint to 50 meters square. How much "paint" will be wasted? - Dimensions of the frame
 The picture frame is made of a 6 cm wide bar. The dimensions of the image are 74 and 57 cm. Are the inner and outer edges of the frame two similar baffles?
The picture frame is made of a 6 cm wide bar. The dimensions of the image are 74 and 57 cm. Are the inner and outer edges of the frame two similar baffles? - Prism
 The prism's base is a rhombus with a side 17 cm and a height 5 cm long. The height of the prism is 88% longer than the side length of the rhombus. Calculate the volume of the prism.
The prism's base is a rhombus with a side 17 cm and a height 5 cm long. The height of the prism is 88% longer than the side length of the rhombus. Calculate the volume of the prism. - Twenty percent
 The students in the class agreed to make various decorative cone-shaped hats for the carnival. How much decorative material did a class of 25 students need to make the hats, if they had to count on about twenty percent waste when cutting and gluing? (The
The students in the class agreed to make various decorative cone-shaped hats for the carnival. How much decorative material did a class of 25 students need to make the hats, if they had to count on about twenty percent waste when cutting and gluing? (The - Cube construction
 A 2×2×2 cube will be constructed using four white and four black unit cube. How many different cubes can be constructed in this way? ( Two cubes are not different if one can be obtained by rotating the other. )
A 2×2×2 cube will be constructed using four white and four black unit cube. How many different cubes can be constructed in this way? ( Two cubes are not different if one can be obtained by rotating the other. ) - Cone mesh drawing
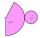 Sketch the cone mesh and add the side length, the arc length of the circle, and the circle length to it, if you know: the side length of the cone: s = 51.9 cm cone base circumference = O = 151 mm.
Sketch the cone mesh and add the side length, the arc length of the circle, and the circle length to it, if you know: the side length of the cone: s = 51.9 cm cone base circumference = O = 151 mm. - Aquarium water liters
 We are to fill an aquarium with a bottom dimension of 30 cm x 30 cm with water. How many liters of water will we need if we pour water to a height of 20 cm?
We are to fill an aquarium with a bottom dimension of 30 cm x 30 cm with water. How many liters of water will we need if we pour water to a height of 20 cm? - Cube substance density
 What kind of substance is it if it is enclosed in a cube with a volume of 8 m³ weighing 110 kg and the entire cube weighs 115.78 kg?
What kind of substance is it if it is enclosed in a cube with a volume of 8 m³ weighing 110 kg and the entire cube weighs 115.78 kg? - Perimeter of needle
 The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area.
The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area. - Rectangle dimensions
 The rectangle has a circumference of 24 cm so that its area is maximum and its length is larger than its width. Find the dimensions of a rectangle.
The rectangle has a circumference of 24 cm so that its area is maximum and its length is larger than its width. Find the dimensions of a rectangle. - Cube surfaces ratio
 The volumes of the two cubes are in the ratio of 27:8. What is the ratio of the surfaces of these cubes?
The volumes of the two cubes are in the ratio of 27:8. What is the ratio of the surfaces of these cubes? - How many
 How many m² of copper sheet is needed to replace the roof of a conical tower with a diameter of 13 meters and a height of 24 meters if we count 8% of the material for bending and waste?
How many m² of copper sheet is needed to replace the roof of a conical tower with a diameter of 13 meters and a height of 24 meters if we count 8% of the material for bending and waste? - The observatory
 The dome of the hemisphere-shaped observatory is 5.4 meters high. How many square meters of sheet metal need to be covered to cover it, and must we add 15 percent to the minimum amount due to joints and waste?
The dome of the hemisphere-shaped observatory is 5.4 meters high. How many square meters of sheet metal need to be covered to cover it, and must we add 15 percent to the minimum amount due to joints and waste?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
