Solid geometry, stereometry - page 111 of 121
Number of problems found: 2409
- Vertical prism
The base of the vertical prism is a rhombus with diagonals of 24 cm and 10 cm. Suppose the shell area is 52% of the total surface area of the prism. Calculate its surface. - Air mass
What is the weight of the air in a classroom with dimensions 10 m × 3 m × 3 m? The air density is 1.293 kg/m³. - Kilograms 66864
The sculptor composes an ice city from ice cubes. The cube with an edge length of 2 dm weighs 7.2 kg. How many kilograms is an ice cube with an edge length of 6 dm heavier than it? - Brass tube
The outer perimeter of the brass tube (ρ = 8.5 g/cm³) is 38 cm. Its mass is 5 kg, length 54 cm. What is the pipe wall thickness? - Cube in sphere
The cube is inscribed in a sphere with a radius r = 6 cm. What percentage is the cube's volume from the ball's volume? - Approximately 44981
The largest Egyptian pyramid has the shape of a regular four-sided pyramid with a base edge of approximately 227 meters and a height of about 140 meters. How many tons of stone did the workers transport to build it? One cube of stone weighs 2500 kg and ne - MO SK/CZ Z9–I–3
John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball. - Transforming cuboid
A cuboid with dimensions 6 cm, 10, and 11 cm is converted into a cube with the same volume. What is its edge length? - Volume 33051
We have two cubes of the same weight. One is all made of glass, the other of cork. Which one has more volume, and how many times? - Lampshade
The cone-shaped lampshade has a diameter of 30 cm and a height of 10 cm. How many cm² of material will we need when 10% is waste? - Rectangular cuboid
The rectangular cuboid has a surface area 4131 cm², and its dimensions are in the ratio 2:4:5. Find the volume of this rectangular cuboid. - Equilateral 81142
The rotating body was created by rotating an equilateral triangle with a side length of a=2 cm around one of its sides. Calculate the volume of this rotating body. - Similarity
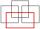Rectangle ABCD has dimensions of 7 cm and 8 cm. Rectangle PQRS has dimensions 7 cm and 6 cm. Determine the coefficient of the similarity k of the rectangles; if they aren't similar, enter zero as the coefficient of similarity. - Logs
The trunk diameter is 52 cm. Is it possible to inscribe a square prism with a side 27 cm? - Quadrilateral 4S prism
The edge lengths of a quadrilateral prism are in the ratio a:b:c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Tower Charles built a tower of cubes with an edge 2 cm long. In the lowest layer, there were six cubes (in one row) in six rows. In each subsequent layer, always one cube and one row less. What volume in cm³ did the whole tower have?
- Three-sided prism
Find the area of the largest wall of a three-sided prism, with a height of 4 dm and an edge length of 5 cm and 6 cm. - Cube edges length
If we reduce the length of the cube edge by 30%, this reduced cube has an area of 1176 cm². Specify the edge length and volume of the original cube. - Calculate 4842
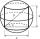The area of the rotating cylinder shell is half the area of its surface. Calculate the surface of the cylinder if you know that the diagonal of the axial section is 5 cm. - Determine: 10182
The lengths of the edges of two cubes are in the ratio 1:2, determine: a) the ratio of the area of the wall of the smaller cube to the area of the wall of the larger cube. b) the ratio of the surface of the smaller cube to the surface of the larger cube.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
