Solid geometry, stereometry - page 97 of 121
Number of problems found: 2404
- Centimeters 4178
Find the surface of a block whose one wall is 48 centimeters square and the other wall is 30 centimeters square. - Circumference 81557
Calculate how many volleyballs with a circumference of 65 cm fit into a cube-shaped rack whose edge is 100 cm long. - Cornbreads
If four and a half teaspoons of baking powder are needed to make ten servings of cornbread, how many teaspoons are needed to make 25 servings? - Volume and body diagonal
Calculate how much the cuboid's volume and body diagonal decrease if we reduce each of its three edges, a, b, and c, by 18%. - Consider
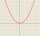Consider all square prisms with a height of 10 cm. If x is the measurement of the base edge in cm, and y is the prism's volume in cm³. Graph the function - Ratio
The radii of the two cones are in the ratio of 5:7. Calculate the volume ratio of cones that have the same height. - Air bubble
The air bubble at the bottom of the lake at a depth of h = 21 m has a radius of r1 = 1 cm at a temperature of t1 = 4°C. The bubble rises slowly to the surface, and its volume increases. Calculate its radius when it reaches the lake's surface, with a tempe - Cardboard box
We want to make a cardboard box-shaped quadrangular prism with a rhombic base. The rhombus has a side of 5 cm and 8 cm, one diagonal long. The height of the box is 12 cm. The box will be open at the top. How many square centimeters do we need if we calcul - Into box
How many cubes with an edge of 2.5 cm fit into a box measuring 11.6 cm, 8.9 cm, and 13.75 cm? - Twice of radius
How many times does the surface of a sphere decrease if we reduce its radius twice? - Cuboid enlargement
By how many percent increases the volume of the cuboid if every dimension increases by 30%? - Minimum surface
Find the length, breadth, and height of the cuboid-shaped box with a minimum surface area into which 50 cuboid-shaped blocks, each with length, breadth, and height equal to 4 cm, 3 cm, and 2 cm, respectively, can be packed. - Cuboid
The sum of the lengths of the three edges of the cuboid that originate from one vertex is 210 cm. The edge length ratio is 7:5:3. Calculate the length of the edges. - Perpendicular 82488
For the volumes of a perpendicular prism and a pyramid with the same base and height: A) the volumes are equal B) the volume of a pyramid is three times smaller than the volume of a prism C) the ratio of the volumes of the prism and the pyramid is 1:3 D) - Volume of three cuboids
Calculate the total volume of all cuboids for which the edges' sizes are in a ratio of 1:2:3, and one of the edges has a size of 6 cm. - Lathe
Calculate the percentage of waste if the cube with 44 cm long edge is lathed to the cylinder with a maximum volume. - Lathe
From the cube of edge, 41 cm was a lathed maximum cylinder. What percentage of the cube is left as waste after being lathed? - Efficiency 35023
The cellar, which has a floor area of 50 m² and is 3 m below ambient level, was flooded with water to a height of 80 cm. How long does it take for a pump with a power input of 1 kW and an efficiency of 75% (η = 0.75) to drain the water? - Hole
They fill the shape hole with dimensions 2.7 m, 20 m, 15.8 m with 282 m³ of soil. How much percent does it fill up? - The wooden The wooden block measures 12 cm, 24 cm, and 30 cm. Peter wants to cut it into several identical cubes. At least how many cubes can he get?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
