Square practice problems - page 140 of 150
Number of problems found: 3000
- Same area
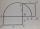 There is a given triangle. Construct a square of the same area.
There is a given triangle. Construct a square of the same area. - Secret treasure
 Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base of 4 m and a height of 3 m. Find the container's radius r (and height h) so that they can hide the largest possible treasure.
Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base of 4 m and a height of 3 m. Find the container's radius r (and height h) so that they can hide the largest possible treasure. - Cube Surface from Section
 The cube A B C D A'B'C'D 'has a section area ACC'A' equal to 64 square root of 2 cm². Calculate the surface of the cube.
The cube A B C D A'B'C'D 'has a section area ACC'A' equal to 64 square root of 2 cm². Calculate the surface of the cube. - Body diagonal
 Cuboid with base 7cm x 3,9cm and body diagonal 9cm long. Find the height of the cuboid and the length of the diagonal of the base,
Cuboid with base 7cm x 3,9cm and body diagonal 9cm long. Find the height of the cuboid and the length of the diagonal of the base, - Inscribed rectangle
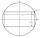 The circle area is 231. Determine the area of the inscribed rectangle with one side 13 long.
The circle area is 231. Determine the area of the inscribed rectangle with one side 13 long. - Square quadrilateral area
 The picture shows a square ABCD with the center S and the side 8 cm long. Point E is any point on the CD side other than C and D. Calculate the area of the ASBE quadrilateral in cm².
The picture shows a square ABCD with the center S and the side 8 cm long. Point E is any point on the CD side other than C and D. Calculate the area of the ASBE quadrilateral in cm². - Pool whitewashing
 The pool is in the shape of a vertical prism with a bottom in the shape of an isosceles trapezoid with dimensions of the bases of the trapezoid 10m and 18m, and arms 7m are 2m deep. During spring cleaning, the bottom and walls of the pool must be whitewas
The pool is in the shape of a vertical prism with a bottom in the shape of an isosceles trapezoid with dimensions of the bases of the trapezoid 10m and 18m, and arms 7m are 2m deep. During spring cleaning, the bottom and walls of the pool must be whitewas - Roof material calculation
 How much sheet is needed for a roof with the shape of a regular quadrilateral pyramid if its edge is 2.8 m long and the height of the roof is 0.8 m? Calculate 10% for the overlap (extra).
How much sheet is needed for a roof with the shape of a regular quadrilateral pyramid if its edge is 2.8 m long and the height of the roof is 0.8 m? Calculate 10% for the overlap (extra). - Quadrilateral pyramid
 The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place.
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Triangular prism
 The plane passing through the edge AB and the center of segment CC' of regular triangular prism ABCA'B'C' has an angle with base 30 degrees, |AB| = 15 cm. Calculate the volume of the prism.
The plane passing through the edge AB and the center of segment CC' of regular triangular prism ABCA'B'C' has an angle with base 30 degrees, |AB| = 15 cm. Calculate the volume of the prism. - Circles 2
 Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 29 cm, 16 cm, and 21 cm.
Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 29 cm, 16 cm, and 21 cm. - Roof cardboard
 The roof of the prefabricated holiday cottage has the shape of a regular quadrilateral pyramid with a length of the base edge of 8 meters and a height of 9 m. How many square meters of cardboard are needed to cover the roof?
The roof of the prefabricated holiday cottage has the shape of a regular quadrilateral pyramid with a length of the base edge of 8 meters and a height of 9 m. How many square meters of cardboard are needed to cover the roof? - Square triangle area
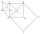 The figure shows the squares ABCD, EFCA, CHCE, and IJHE. Points S, B, F, and G are, respectively, the centers of these squares. Line segment AC is 1 cm long. Determine the area of triangle IJS. Please help...
The figure shows the squares ABCD, EFCA, CHCE, and IJHE. Points S, B, F, and G are, respectively, the centers of these squares. Line segment AC is 1 cm long. Determine the area of triangle IJS. Please help... - Construct
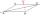 Construct a rhombus ABCD if the size of the diagonal AC is 6 cm and the diagonal BD is 8 cm long.
Construct a rhombus ABCD if the size of the diagonal AC is 6 cm and the diagonal BD is 8 cm long. - Cone Lateral Surface Area
 Calculate the cone shell with a base diameter of 40 cm and a cone height of 50 cm.
Calculate the cone shell with a base diameter of 40 cm and a cone height of 50 cm. - Quadrilateral prism
 Calculate the surface and volume of a quadrilateral prism if given: the area of the base is 40 cm square, the bottom of the base is k = 8 cm, and the height of the prism is 1.3 dm (the bottom is a rectangle)
Calculate the surface and volume of a quadrilateral prism if given: the area of the base is 40 cm square, the bottom of the base is k = 8 cm, and the height of the prism is 1.3 dm (the bottom is a rectangle) - Digging a pit
 The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit.
The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit. - Box
 The cardboard is a box-shaped quadrangular prism with a rhombic base. Rhombus has a side 5 cm, one diagonal 8 cm long, and the box's height is 12 cm. The package will open at the top. How many cm² of cardboard do we need to cover overlap and joints that a
The cardboard is a box-shaped quadrangular prism with a rhombic base. Rhombus has a side 5 cm, one diagonal 8 cm long, and the box's height is 12 cm. The package will open at the top. How many cm² of cardboard do we need to cover overlap and joints that a - A rhombus 4
 A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution.
A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution. - Pentagon
 Calculate the length of a regular pentagon's side, circumference, and area, inscribed in a circle with a radius r = 6 cm.
Calculate the length of a regular pentagon's side, circumference, and area, inscribed in a circle with a radius r = 6 cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
