Square practice problems - page 141 of 150
Number of problems found: 3000
- The bus stop
 The bus stop waiting room has the shape of a regular quadrilateral pyramid 4 m high with a 5 m base edge. Calculate how much m² roofing is required to cover the sheathing of three walls, taking 40% of the additional coverage.
The bus stop waiting room has the shape of a regular quadrilateral pyramid 4 m high with a 5 m base edge. Calculate how much m² roofing is required to cover the sheathing of three walls, taking 40% of the additional coverage. - Rectangle - parallelogram
 A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle.
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle. - Diagonals in diamond
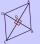 In the rhombus, a = 160 cm and alpha = 60 degrees are given. Calculate the length of the diagonals.
In the rhombus, a = 160 cm and alpha = 60 degrees are given. Calculate the length of the diagonals. - The coil
 How many ropes (a diameter of 8 mm) fit on the coil (threads are wrapped close together)? The coil has the following dimensions: The inner diameter is 400mm. The outside diameter is 800mm. The length of the coil is 470mm.
How many ropes (a diameter of 8 mm) fit on the coil (threads are wrapped close together)? The coil has the following dimensions: The inner diameter is 400mm. The outside diameter is 800mm. The length of the coil is 470mm. - Tunnel - quadrilateral
 How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral.
How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral. - The fence
 I'm building a cloth (board) fence. The boards are rounded in a semicircle at the top. The tops of the boards between the columns should copy an imaginary circle. The tip of the first and last board forms the chord of a circle whose radius is unknown. The
I'm building a cloth (board) fence. The boards are rounded in a semicircle at the top. The tops of the boards between the columns should copy an imaginary circle. The tip of the first and last board forms the chord of a circle whose radius is unknown. The - Hexagon cut pyramid
 Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm.
Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm. - Central angle
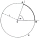 A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long.
A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long. - Diagonals
 Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°.
Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°. - Cone cutout
 The cone shell with a base radius of 20 cm and a height of 50 cm unfolds into a circular cutout. How big is the center angle of this cutout?
The cone shell with a base radius of 20 cm and a height of 50 cm unfolds into a circular cutout. How big is the center angle of this cutout? - Rhombus
 It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus.
It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus. - Hexagonal prism volume
 A perpendicular hexagonal prism was created by machining a cube with an edge length of 8 cm. The base of the prism is created from the square wall of the original cube by separating 4 identical right triangles with overhangs of lengths 3cm and 4cm. The he
A perpendicular hexagonal prism was created by machining a cube with an edge length of 8 cm. The base of the prism is created from the square wall of the original cube by separating 4 identical right triangles with overhangs of lengths 3cm and 4cm. The he - Arch ground length
 The arch has a radius of 3.3 m, a span of 3.25 m, and a height of 20 cm above the ground. What is the length of the arc to reach the ground?
The arch has a radius of 3.3 m, a span of 3.25 m, and a height of 20 cm above the ground. What is the length of the arc to reach the ground? - Hexagonal pyramid
 The pyramid's base is a regular hexagon, which can be circumscribed in a circle with a radius of 1 meter. Calculate the volume of a pyramid 2.5 meters high.
The pyramid's base is a regular hexagon, which can be circumscribed in a circle with a radius of 1 meter. Calculate the volume of a pyramid 2.5 meters high. - Cube
 Calculate the cube ABCDA'B'C'D's surface if the area of rectangle ACC'A' = 344 mm².
Calculate the cube ABCDA'B'C'D's surface if the area of rectangle ACC'A' = 344 mm². - Ratio of squares
 A circle is given, and a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares?
A circle is given, and a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares? - Given is
 Given is the circle x²+y²-4x+2y-11=0. Calculate the area of the regular hexagon inscribed in the given circle.
Given is the circle x²+y²-4x+2y-11=0. Calculate the area of the regular hexagon inscribed in the given circle. - Quadrilateral prism
 Calculate the volume and surface of a regular quadrilateral prism with a base edge a = 46 mm and a height v = 0.67 dm.
Calculate the volume and surface of a regular quadrilateral prism with a base edge a = 46 mm and a height v = 0.67 dm. - Square
 Square JKLM has sides of a length of 24 cm. Point S is the center of LM. Calculate the area of the quadrant JKSM in cm².
Square JKLM has sides of a length of 24 cm. Point S is the center of LM. Calculate the area of the quadrant JKSM in cm². - Heptagonal pyramid
 A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³.
A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
