Triangle practice problems - page 27 of 125
Number of problems found: 2496
- Elevation of the tower
We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39°25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56°42''. How tall is the tower - Depth angle
Determine the height of the cloud above the lake's surface if we see it from place A at an elevation angle of 20° 57'. From the same place A, we see its image in the lake at a depth angle of 24° 12'. Observation point A is 115 m above the lake level. - Map - climb
On the map of the High Tatras, on a scale of 1:11000, are cable car stations in the Tatranska Lomnica and the Skalnate Pleso with a distance of 354.6 mm. The altitude of these stations is 949 m and 1760 m. What is the average angle of climb on this cable - Complex square roots
Determine the sum of the three square roots of 343. - The chimney
How high is the chimney if we see it from a distance of 60 m at an angle of 42°? - Right triangle
It is given a right triangle angle alpha of 90 degrees the beta angle of 55 degrees c = 10 cm use the Pythagorean theorem to calculate sides a and b - Inclined plane
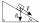1. How much work W do we have to do to pull a body weighing 200 kg along an inclined plane with a length of 4 m to a total height of 1.5 m? 2. Find the force we need to exert to do this if we neglect frictional resistance. 3. Find the force we would need - goniometric functions
Based on the fact that you know the values of sin and cos of a given angle and you know that tan (tangent) is their ratio, determine d) tan 120 ° e) tan 330 ° - Fighter
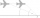A military fighter flies at an altitude of 10 km. The ground position was aimed at an altitude angle of 23° and 12 seconds later at an altitude angle of 27°. Calculate the speed of the fighter in km/h. - Centimeters 19103
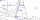Emma was raking leaves in the garden. During lunch, she leaned the 170 cm long rake against a tree, with the upper end reaching a height of 90 cm. How far from the tree was the bottom of the rake? Enter the result in whole centimeters. - Triangle α and side
Side a in the right triangle has size a = 120 mm, angle α = 60°. How big is the hypotenuse c? - Tree
Between points A and B is 50m. From A, we see a tree at an angle of 18°. From point B, we see the tree at a three times bigger angle. How tall is a tree? - Complex roots
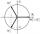Find the sum of the fourth square root of the number 16. - Two groves
Two groves A and B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'? - Cablecar
Funicular on Petrin (Prague) was 408 meters long and overcame the difference of 106 meters in altitude. Calculate the angle of the climb. - Two cyclists
Two cyclists started crossing at the same time. One goes to the north speed of 20 km/h, the second eastward at a speed of 26 km/h. What will be the direct distance cycling 30 minutes from the start? - Rectangular
Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle - Horizontally 6296
The camera with a viewing angle of 120 ° was placed horizontally on the observatory at 30 m. What length d of the section at the tower's base can the camera not capture? - Perpendicular 5712
Adam and Boris go from school on two perpendicular paths. Adam's average speed is 6 km/h, and Borisova's is 8 km/h. How far will they be by air for 0.5 hours? - Rectangular triangle PQR
In the rectangular triangle PQR, the PQ leg is divided by the X point into two segments, of which longer is 25cm long. The second leg PR has a length of 16 cm. The length of the RX is 20 cm. Calculate the length p of side RQ. The result is round to 2 deci
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
