Faktoriál - príklady - strana 2 z 7

Pokyny: Každý problém vyriešte opatrne a krok za krokom napíšte, ako ste ho vyriešili.

Počet nájdených príkladov: 134

Peter 21
Peter, Jano, Alica a Rebeka išli na koncert vážnej hudby. Koľkými rôznými spôsobmi sa môžu usadiť na štyri voľné sedadlá ak Rebeka chce sedieť pri Janovi?
Mier
V ostatných dňoch mám často pred očami hlavne dve farby - modrú a žltú. Je mi smutno z toho, čo sa deje. Preto aj dnes mám pre vás úlohu o farbách. V peračníku mám 5 fixiek: modrú, žltú, zelenú, červenú a fialovú. Koľko mám možností ich v peračníku uložiť
Máme 2
Máme 2 rovnaké modré guľôčky a 2 rovnaké červené guľôčky. Usporiadame ich všetkými spôsobmi do radu. Koľko rôznych usporiadaní existuje?
Petra 6
Petra si na začiatku letných prázdnin vypožičala z knižnice štyri knihy. Koľko je poradí, v ktorých ich postupne mohla prečítať?
Slovo JAMA
Koľko rôznych štvorpísmenových slov sa dá vytvoriť z písmen slova JAMA?
Marián
Marián dostal v priebehu jedného dňa dve rôzne známky. Koľko je možností pre známky, ktoré mohol dostať?
V počítačovej
V počítačovej hre je potrebné pozbierať v miestnosti 5 predmetov: meč, prsteň, obraz, kľúč a mincu. Záleží na poradí, v akom jednotlivé predmety pozbierame, pri zlom poradí prídeme o život . Koľko je všetkých poradí?
Vystavenie šampónov
Koľkým spôsobom môže aranžérka vystaviť vodorovne vedľa seba 5 rôznych šampónov?
Paličky - trojuholník
Boulder Bob má veľa palíc s dĺžkou 3,5 a 7. Chce tvoriť trojuholníky, z ktorých každý okraj pozostáva práve z jednej palice. Koľko nezhodných trojuholníkov možno vytvoriť pomocou tyčiniek?
Usporiadanie kníh
Kníhkupectvo Lacný Jožko znižuje ceny kníh o matematike na propagáciu. Obchod má 6 kníh o algebre, 6 kníh o geometrii a 5 kníh o štatistike, ktoré sa dajú usporiadať na policu. Knihy rovnakého druhu sa umiestnia vedľa seba. Koľkými spôsobmi môžu byť tieto
Morzeovka
Koľko znakov môžeme vytvoriť z dvoch čiarok a štyroch bodiek?
Permutácie s opakovaním
Určte počet usporiadaní týchto šiestich prvkov: a, a, a, b, b, c.
Šesť chlapcov
Šesť chlapcov a šesť dievčat (medzi nimi Emil, Félix, Gertrúda a Hanka) si chcú zatancovať. Počet spôsobov, ako môžu vytvoriť šesť (zmiešaných) párov, pokiaľ Emil nechce tancovať s Gertrúdou a Hanka chce tancovať s Félixom je?
V skupine 2
V skupine je 5 dievčat a 7 chlapcov. Sedia v rade vedľa seba. Koľko je možností, ak žiadne 2 dievčatá nebudú sedieť vedľa seba.
Vlajka 2
Vlajka má byť zložená z 3 rôznofarebných vodorovných pruhov. K dispozícii sú farby: biela, červená, modrá, zelená a žltá. Určte: A) počet všetkých vlajok B) počet vlajok s modrým pruhom C) počet vlajok s modrým pruhom v strede D) počet vlajok, ktoré NEmaj
Koľkými 11
Koľkými rôznymi spôsobmi môžme usadiť troch ľudí na tri stoličky, štyroch na štyri, piatich na päť a šiestich na šesť stoličiek? Nájdite spoločné vlastnosti pri výbere objektov z hľadiska kombinatoriky. Zistite princip výpočtu všetkých možností spĺňajúcic
Postavenie veží
Koľkými spôsobmi môžeme na šachovnici 8×8 postaviť 8 nerozlíšiteľných veží tak, aby sa neohrozovali?
Zápis bez exponentu
Koľkými spôsobmi možno zapísať x³ y⁴ z³ bez exponentu?
Vybrať komisiu
Na oddelení je sedem žien a päť mužov. a) koľkými spôsobmi možno vybrať výbor zložený z 3 osôb? b) koľkými spôsobmi možno vybrať komisiu 2 mužov a jednej ženy? c) koľkými spôsobmi možno vybrať výbor zložený z najmenej dvoch žien (spolu 3 osoby)?
S faktoriálom
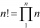Vykráť výraz s faktoriálmi: 12! x 2 x 7! / 6 x 10! 8!

Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.